Procedimenti geometrici per la costruzione delle tangenti
a una parabola uscenti da un punto |
Teorema 1
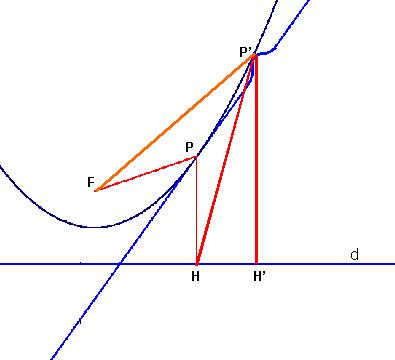
Data una parabola di fuoco F e direttrice d e chiamato H la proiezione ortogonale di un
suo punto P sulla direttrice d, la bisettrice dell’angolo FPH è la tangente in nel
punto P alla parabola. |
Dim.
Tracciata la bisettrice come da enunciato si osserva che essa non può avere un altro
punto P’ in comune con la parabola, se così fosse:
- P’H sarebbe congruente a P’F perché P’ appartiene
all’asse di FH (il triangolo FPH è isoscele per la definizione di parabola come
luogo di punti, quindi la bisettrice dell’angolo al vertice è anche asse della base).
- Chiamata H’ la proiezione ortogonale di P’ sulla direttrice
dovrebbe anche essere P’H’ congruente a P’F (perché P’ appartiene
alla parabola), per la proprietà transitiva della congruenza si avrebbe allora
P’H congruente a P’H’
- Se ora si considera il triangolo P’HH’, rettangolo in H’,
si giunge all’assurdo che esisterebbe un triangolo rettangolo con l’ipotenusa
congruente a un cateto.
Questo teorema permette di costruire con riga e compasso
la tangente ad una circonferenza in un suo punto
Dal punto di vista analitico permette di trovare
l’equazione di tale tangente senza utilizzare la condizione di tangenza. |
 |
Teorema 2 (di Zanzottera)
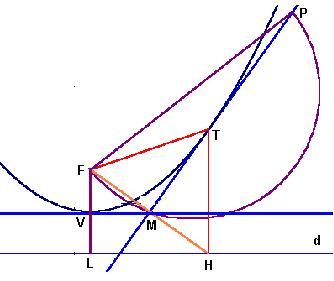
Le rette tangenti ad una parabola di fuoco F, uscenti da un punto P ad essa
esterno, passano per i punti che si ottengono intersecando la circonferenza di diametro PF
con la parallela alla direttrice passante per il vertice. |
Dim.
Tracciamo la retta tangente alla parabola in T, uscente da P e
indichiamo con H la proiezione ortogonale di T sulla direttrice d, il triangolo FTH è
isoscele su FH (per la definizione di parabola come luogo di punti), mentre la
retta PT è bisettrice dell’angolo FTH (per il teorema precedente). Chiamato M
il punto di intersezione del segmento FH con la retta PT, possiamo affermare che TM altre
ad essere bisettrice del triangolo FHT è anche mediana e altezza, il punto M allora
apparterrà alla semicirconferenza di diametro PF (perché essendo PFM un triangolo
rettangolo è inscrittibile in una semicirconferenza).
Consideriamo adesso il triangolo FHL, dove L è la proiezione ortogonale
di F sulla direttrice, per il teorema di Talete la parallela all direttrice che passa per
il vertice V (punto medio di FL) passa anche per M.
Possiamo allora concludere che M appartiene alla circonferenza di
diametro PF (punto 1) e alla parallela alla direttrice che passa per V (punto 2)
c.v.d.
|
|

