Nel capitolo precedente abbiamo analizzato il
funzionamento di una rete neurale strutturata
come memoria associativa. Ricordiamo che una
memoria associativa realizzata con tecnica
neurale deve presentare una delle seguenti
proprietà:
-un contenuto parzialmente corretto in input
deve richiamare comunque l'output associato
corretto
-un contenuto sfumato o incompleto
in input deve trasformarsi in un contenuto
corretto e completo in output
Quando parliamo di contenuto dell'input di una
memoria associativa intendiamo una configurazione
di valori booleani ai quali pero possiamo dare
significati più articolati tramite opportune
interfacce software sugli input/output della rete.
Le memorie associative analizzate hanno comunque una serie
di limitazioni abbastanza gravi:
1)capacità di memoria bassa
2)spesso è necessaria ortogonalità dei vettori di input
3)le forme riconosciute devono essere linearmente separabli
4)incapacità di adattamento alla traslazione,all'effetto
scala e alla rotazione.
5)possibilità di operare solo con dati booleani.
Spieghiamo meglio i punti 3 e 4 che forse possono risultare
i più oscuri:
-la separabilità lineare di una forma da riconoscere
si ha quando una retta(in due dimensioni) o un piano
(in tre dimensioni) o un iperpiano(in n dimensioni)
puo` separare i punti X(k)={x1(k),x2(k),...xn(k)}
(corrispondenti alla forma k da riconoscere) da tutti
gli altri punti che rappresentano forme differenti
e quindi da discriminare.
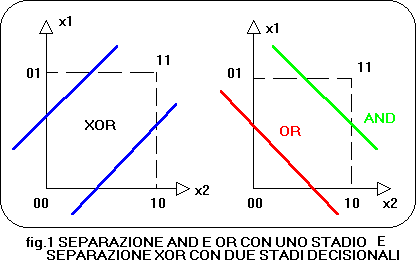
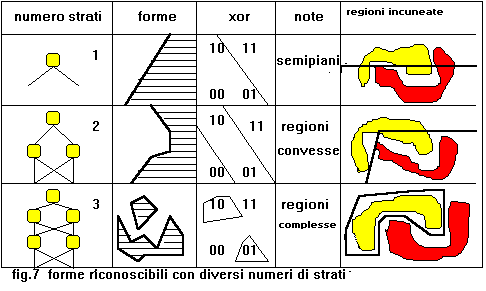
Ad esempio le due forme logiche AND e OR sono linearmente
separabili,mentre non lo e` la forma logica XOR
(or esclusivo), come rappresentato in fig.1.
-l'incapacità di adattamento alla traslazione e alla
rotazione o all'effetto scala è importante nel
riconoscimento di immagini di oggetti che dovrebbero
potere essere riconosciuti indipendentemente da questi
tre fattori.

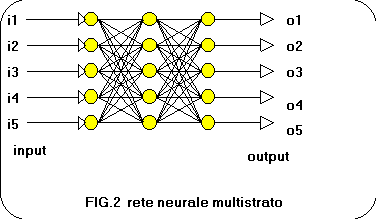
RETI NEURALI MULTISTRATO
Prossimamente ci occuperemo di reti neuronali che non sono impiegate come memorie associative ma sono in grado di svolgere funzioni più complesse, quali il riconoscimento di forme qualsiasi e la estrapolazione di correlazioni tra insiemi di dati apparentemente casuali. Nel fare questo passaggio dalle memorie associative alle reti multistrato tralasciamo il Perceptron, un tipo di rete neurale a due strati che ha senz'altro una importanza storica come capostipite delle attuali reti backprop e che vale la pena di menzionare. Il tipo di reti neurali che analizzeremo è unidirezionale nel senso che i segnali si propagano solamente dall'input verso l'output senza retroazioni che sono invece presenti nella memoria associativa BAM vista nel capitolo precedente(ricordate che la rete raggiungeva la stabilita` come minimo energetico quando le oscillazioni dovute alla retroazione erano completamente smorzate?). Nel tipo di reti che vedremo i neuroni possono assumere valori reali (compresi tra 0.0 e 1.0) e non più valori booleani 0 e1 per cui la flessibilità della rete risulta nettamente migliorata nella applicabilità a problemi reali. Ogni neurone di ogni strato sara collegato ad ogni neurone dello strato successivo, mentre non vi saranno collegamenti tra i neuroni dello stesso strato(fig.2) . Quella di figura 2 è la configurazione più semplice di rete multistrato, dotata di un solo strato intermedio normalmente chiamato "hidden layer": gli strati decisionali di tale rete sono lo strato intermedio e lo strato di output. Questa è un affermazione che puo sembrare scontata ma qualcuno di voi si sara chiesto:"perche lo strato di neuroni di input non ha potere decisionale?" Ottima domanda! Facciamo un passo indietro ricordando che la memoria associativa del capitolo precedente imparava gli esempi dell' addestramento attraverso un particolare algoritmo che modificava i pesi dei collegamenti tra i neuroni. Cio che una rete neurale impara sta proprio nel valore dei pesi che collegano i neuroni opportunamente modificato in base ad una legge di apprendimento su un set di esempi. Allora comprendiamo che lo strato di input non è uno strato decisionale perche non ha pesi modificabili in fase di apprendimento sui suoi ingressi.
E{K=1,N}(K) X(K) INDICA SOMMATORIA DI INDICE K
DI X DA K=1 A K=N
(i limiti possono non essere presenti.Es: E(k) X(k)*Y(j))
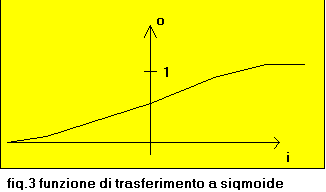
Ogni neurone ha una precisa funzione di trasferimento come avevamo gia accennato parlando delle memorie associative nelle quali i neuroni hanno una funzione di trasferimento a gradino. In una rete error_back_propagation dove vogliamo avere la possibilita` di lavorare con valori reali e non booleani,dobbiamo utilizzare una funzione di trasferimento a sigmoide (fig.3)definita dalla formula:
O = 1/(1+exp(-I))
dove O=output del neurone, I=somma degli input del neurone
e in particolare I= E{k=1,n}(k) w(j)(k) * x(k)
La sigmoide di fig.3 e` centrata sullo zero ma in molte applicazioni e` decisamente opportuno che il centro delle sigmoidi di ogni neurone sia "personalizzato" dal neurone stesso per garantire una maggiore flessibilità di calcolo. Si puo` ottenere cio` modificando l'ultima formula nel seguente modo:
I= E{k=1,n}(k) w(j)(k) * x(k) - S(k)
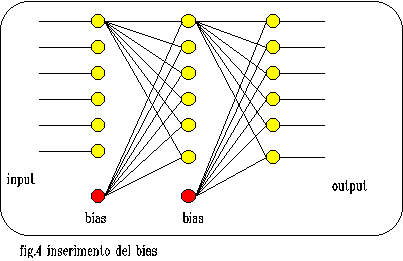
dove S(k) è il punto in cui è centrata la sigmoide del k_esimo neurone. Affinche tale soglia sia personalizzata è necessario che essa venga appresa(cioè si modifichi durante la fase di apprendimento) esattamente come i pesi delle connessioni tra i neuroni dei diversi strati. Con un piccolo trucco possiamo considerare tale soglia come un input aggiuntivo costante al valore 1 che è collegato al neurone k con un peso da "apprendere": la nostra rete si trasforma pertanto in quella di fig.4. La formula per cacolare l'attivazione del neurone diventa:
I=E{k=1,n+1}(k) w(j)(k) * x(k)
Il tipo di addestramento che si esegue su questa rete
è chiamato "supervised" (supervionato) perchè
associa ogni input ad un output desiderato:
ciclo epoche:
{
per ogni esempio:
{
a)si fornisce l'input alla rete
b)si preleva l'output da questa fornito
c)si calcola la differenza con l'output desiderato
d)si modificano i pesi di tutti i collegamenti
tra i neuroni in base a tale errore con una
regola (chiamata regola delta) in modo che tale
errore diminuisca.
}
e)calcolo dell'errore globale su tutti gli esempi
f)si ripete il ciclo epoche finche l'errore non raggiunge
il valore accettato
}
Naturalmente per input e output si intende un insieme di n esempi ciascuno composto da k input (k sono gli input fisici della rete) e j output(j sono gli output fisici della rete). Ogni ciclo come quello sopraesposto viene chiamato "epoca" di apprendimento. Voglio ricordare il concetto che nel capitolo precedente avevamo chiamato "resistenza al rumore" (nel caso di memorie associative) e qui chiameremo "potere di generalizzazione" intendendone la capacità della rete dopo l'addestramento di dare una risposta significativa anche ad un input non previsto negli esempi. In pratica durante l'addestramento, la rete non impara ad associare ogni input ad un output ma impara a riconoscere la relazione che esiste tra input e output per quanto complessa possa essere: diventa pertanto una "scatola nera" che non ci svelerà la formula matematica che correla i dati ma ci permetterà di ottenere risposte significative a input di cui non abbiamo ancora verifiche "sul campo" sia all'interno del range di valori di addestramento (interpolazione), che all'esterno di esso(estrapolazione). Naturalmente l'estrapolazione è più difficoltosa e imprecisa che l'interpolazione e comunque entrambe danno risultati migliori quanto più è completo e e uniformemente distribuito il set di esempi. Potremmo insegnare ad una rete neurale di questo tipo a fare delle somme tra due valori di input fornerndole in fase di apprendimento una serie di somme "preconfezionate" con risultato corretto in un range più vasto possibile: la rete riuscirà a fare somme anche di valori diversi da quelli degli esempi. Addestrare una rete neurale a fare una somma è ovviamente inutile se non per motivi di studio o sperimentali inquanto essa è utile per studiare fenomeni di cui non sia conosciuta la correlazione matematica tra input e output (o sia estremamente complessa).
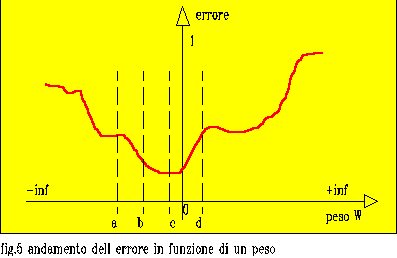
delta_w2=-epsilon*(d err/d w2)
dove d err/d w =derivata dell errore rispetto al peso
epsilon=costante di apprendimento che incide
sulla misura dello spostamento a parita
di "pendenza" nel punto specifico
(e` consiglaibile un valore compreso tra 0.1 e 0.9)
Proviamo a sviluppare questa derivata nel seguente modo:
delta_w2(k)(j)=-epsilon*(d err/d I(j))*(d I(j)/d w2(k)(j))
definendo delta(j)=d err/d I(j) si semplifica in
delta_w2(k)(j)=-epsilon * delta(j) * (d I(j)/d w2(k)(j))
e ricordiamo che la formula di attivazione
di un neurone dello strato di output è
I(j)=E(k) w2(k)(j) * h(k)
dove h(k)=output del neurone k_esimo dello strato hidden
la sua derivata risulta d I(j)/d w2(k)(j)=h(k)
ritorniamo adesso a delta impostando
delta(j)=(d err/d y(j)) * (d y(j)/d I(j))
e risolviamo separatamente le due derivate in essa contenute:
prima derivata) d err/d y(j) = d (((D(j)-y(j))**2)/2)/d y(j) =-(D(j)-y(j))
seconda derivata) d y(j)/d I(j) =d (1/(1+e**(-I(j)))/d I(j) = y(j) * (1-y(j))
per cui dato che
delta_w2(j)=-epsilon * delta(j) * (d I(j)/d (w2(k)(j))
si ha delta_w2=-epsilon * delta(j) * h(k)
e delta(j)=(D(j)-y(j))*y(j)*(1-y(j))
abbiamo la formula che ci consente di calcolare i pesi delle connessioni tra i neuroni dello strato di output e quelli dello strato intermedio:
delta_w2[j][k]=epsilon*(D[j]-y[j]) * y[j] * (1-y[j]) * h[k]
dove conosciamo
D[j] come valore di output desiderato
y[j] come valore di output ottenuto
h[k] come stato di attivazione del
neurone k del livello intermedio
delta_w1[j][k]=-epsilon*(d err / d w1[j][k])
sviluppiamo la derivata nel seguente modo:
delta_w1[j][k]=-epsilon*(d err/d I[k])*(d I[k]/d w1[j][k])
chiamiamo delta[k]=-(d err/d I[k])
e applicando la regola di composizione delle derivate possiamo scrivere
delta[k]=-(d err/d I[j])*(d I[j]/d h[k])*(d h[k]/d I[k])
dove h[k]=attivazione del k_esimo neurone hidden
quindi anche
delta[k]=-(E(j)(d err/d I[j])*(d I[j]/d h[k]))*(d h[k]/d I[k])
dato che l'operatore sommatoria agisce solo sui fattori aggiunti che si annullano.
Notiamo ora che il primo termine (d err/d I[j])=delta[j] che abbiamo incontrato nei calcoli precedenti e che il secondo (d I[j]/d h[k]) puo essere calcolato come
d E(k) w2[k][j]*h[k]/d h[k] = w2[k][j]
mentre il terzo d h[k]/d I[k] = d h[k]/d (1/1+e**(-h[k]) = h[k]*(1-h[k]
otteniamo finalmente:
delta_w1[j][k]= epsilon * delta[k] * x[j]
in cui
x[i]= i_esimo input
delta[k]= (E[j] delta[j] * w2[k][j]) * h[k] * (1-h[k])
in cui
h[k]= attivazione neurone k dello strato hidden (conosciuto ovviamente eseguendo la rete, cioè moltiplicando gli input per i pesi delle connessioni e sommando tutto)
delta[j] = (D[j]-y[j]) * (y[j]) * (1-y[j])
già calcolato nella parte precedente (quella
relativa alla modifica dei pesi tra output e
hidden).
Notate che delta[j] contiene effettivamente la
retropropagazione dell'errore e infatti è l'unico
termine che contiene dati relativi allo strato
di output contenuto nel calcolo del delta_w1.
Il listato contenuto nel dischetto è un programma di prova di reti
neurali error_back_propagation che permette
di addestrare la rete con un file ascii contenente
i dati input e output desiderato in sequenza come
mostrato in fig.6.
fig.6
.2345 input1 esempio1
.3456 input2
.1234 output
.6789 input1 esempio2
.4567 input2
.4567 output
..... ......
.5678 input1 esempioN
.4567 input2
.8976 output
Il programma contiene le seguenti procedure
exec: esegue la rete con un input
back_propagation: esegue la rtropropagazione dell'errore modificando i pesi delle connessioni
ebp_learn: carica i parametri dell addestramento e chiama learn
learn: procedura che esegue l' addestramento della rete nel seguente modo...
ciclo epoche
{
ciclo esempi
{
chiama exec(esecuzione della rete)
chiama back_propagation(modifica pesi)
calcola errore esempio
calcola errore epoca=max(errori esempi)
}
break se errore epoca < errore ammesso
}
input: preleva i dati dal file net.in in test
ouput: inserisce i dati nel file net.out in test
weight_save: salva i pesi della rete su file
load_weight: carica i pesi della rete da file
Bisogna innanzitutto definire i parametri della
rete che sono numero di input e numero di output
(dipendenti ovviamente dal problema applicativo)
e numero di neuroni che vogliamo negli strati
hidden. Esistono delle formule empiriche per
calcolare il numero dei neuroni degli strati
nascosti in base alla complessità del problema
ma, generalmente, è più la pratica che suggerisce
tale numero(spesso è inferiore al numero degli
input e output). Con più neuroni negli strati
hidden l'apprendimento diventa esponenzialmente
più lungo, nel senso che ogni epoca occupa un tempo
maggiore(n_pesi=n_neuroni1*n_neuroni2), ma non è
escluso che il risultato (raggiungimento del target)
venga raggiunto in un tempo simile a causa di una
maggiore efficienza della rete.
Utilizziamo il training set di fig.8 che contiene 40 esempi
normalizzati di somma di due numeri: il programma presentato
in questo capitolo, su una SPARK station, e` arrivato al
raggiungimento del target 0.05 dopo pochi minuti, in circa 4300
epoche con un epsilon(tasso di apprendimento)=0.5 e con quattro
neuroni per ogni strato intermedio(ovviamente n_input=2 e
n_output=1).
Il raggiungimento del target_error 0.02 è stato
ottenuto nelle stesse condizioni all'epoca ~13800.
Se non volete attendere molto tempo e verificare ugualmente la
convergenza della rete potete ridurre il training set a 10
o 20 esempi curando che siano adeguatamente distribuiti
(8 è dato dalla somma 1+7 ma anche 4+4 e 7+1). Con un training set
ridotto la rete converge molto più velocemente ma è chiaro che
il potere di generalizzazione risulta inferiore, per cui presentando
poi alla rete degli esempi fuori dal training set l'errore ottenuto
potrebbe essere molto piu` elevato del target_error raggiunto.
E` buona norma lavorare con delle pause su un numero di epoche
non elevato al fine di poter eventualmente abbassare il tasso di
apprendimento epsilon quando ci si accorge della presenza di
oscillazioni(errore che aumenta e diminuisce alternativamente)
dovute a movimenti troppo lunghi(epsilon alto) intorno ad un
minimo (che speriamo sia il target e non un minimo locale).
Il raggiungimento del target 0.02 è relativamente rapido
mentre da questo punto in poi la discesa verso il minimo è
meno ripida e i tempi diventano più lunghi(è il problema della
discesa del gradiente con movimenti inversamente proporzionali
alla derivata nel punto). Inoltre avvicinandosi al minimo è
prudente utilizzare un epsilon basso per il motivo esaminato prima.
E` sicuramente possibile che un errore target non sia raggiungibile
in tempi accettabili se è troppo basso in relazione alla
complessita` del problema.
In ogni caso bisogna ricordare che le reti neurali non sono
sistemi di calcolo precisi ma sistemi che forniscono risposte
approssimate a inputs approssimati.
Se ripetete due o più volte lo stesso training con gli stessi dati
e gli stessi parametri potreste sicuramente notare differenze di
tempi di convergenza verso il target dovuti al fatto che inizialmente
i pesi della rete sono settati a valori random(procedura weight_starter)
che possono essere più o meno favorevoli alla soluzione del problema.
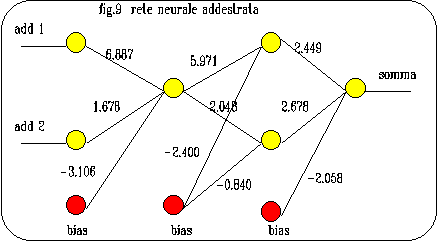
Nella fig.9 è visulizzato il know_how di una rete con un neurone
nello strato hidden1 e due neuroni nello strato hidden2,
dopo l'addestramento alla somma fino al target_error=0.05:
sono evidenziati i numeri che rappresentano i pesi dei collegamenti.
| add1 | add2 | sum | add1 | add2 | sum |
| 0.40 | 0.30 | 0.70 | 0.11 | 0.44 | 0.55 |
| 0.22 | 0.33 | 0.55 | 0.22 | 0.33 | 0.55 |
| 0.37 | 0.37 | 0.74 | 0.33 | 0.22 | 0.55 |
| 0.49 | 0.37 | 0.86 | 0.44 | 0.11 | 0.55 |
| 0.12 | 0.12 | 0.24 | 0.33 | 0.11 | 0.44 |
| 0.11 | 0.11 | 0.22 | 0.22 | 0.22 | 0.44 |
| 0.13 | 0.13 | 0.26 | 0.11 | 0.33 | 0.44 |
| 0.11 | 0.88 | 0.99 | 0.22 | 0.11 | 0.33 |
| 0.22 | 0.77 | 0.99 | 0.11 | 0.11 | 0.22 |
| 0.33 | 0.67 | 1.00 | 0.16 | 0.16 | 0.32 |
| 0.44 | 0.56 | 1.00 | 0.05 | 0.05 | 0.10 |
| 0.55 | 0.45 | 1.00 | 0.77 | 0.11 | 0.88 |
| 0.66 | 0.34 | 1.00 | 0.66 | 0.22 | 0.88 |
| 0.77 | 0.23 | 1.00 | 0.55 | 0.33 | 0.88 |
| 0.88 | 0.12 | 1.00 | 0.44 | 0.44 | 0.88 |
| 0.11 | 0.55 | 0.66 | 0.33 | 0.55 | 0.88 |
| 0.22 | 0.44 | 0.66 | 0.22 | 0.66 | 0.88 |
| 0.33 | 0.33 | 0.66 | 0.11 | 0.77 | 0.88 |
| 0.44 | 0.22 | 0.66 | 0.11 | 0.66 | 0.77 |
| 0.55 | 0.11 | 0.66 | 0.22 | 0.55 | 0.77 |
| inputs | output atteso | output ottenuto | ||||||||||||
| h1 | h2 | h3 | h4 | h5 | M | V | P+ | P- | P0 | m | v | p+ | p- | p0 |
| 0.5 | 0.6 | 0.7 | 0.1 | 0.0 | 1 | 0 | 0 | 0 | 0 | .99 | .00 | .00 | .00 | .00 |
| 0.3 | 0.2 | 0.1 | 0.5 | 0.6 | 0 | 1 | 0 | 0 | 0 | .00 | .99 | .00 | .00 | .00 |
| 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | 0 | 0 | 1 | 0 | 0 | .00 | .00 | .99 | .00 | .00 |
| 0.8 | 0.6 | 0.5 | 0.3 | 0.1 | 0 | 0 | 0 | 1 | 0 | .00 | .00 | .00 | .99 | .00 |
| 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0 | 0 | 0 | 0 | 1 | .00 | .00 | .00 | .00 | .99 |
| 0.4 | 0.5 | 0.6 | 0.4 | 0.3 | 1 | 0 | 0 | 0 | 0 | .99 | .00 | .00 | .00 | .00 |
| 0.6 | 0.5 | 0.3 | 0.4 | 0.7 | 0 | 1 | 0 | 0 | 0 | .00 | .99 | .00 | .00 | .00 |
| 0.4 | 0.5 | 0.7 | 0.8 | 0.9 | 0 | 0 | 1 | 0 | 0 | .00 | .00 | .99 | .00 | .00 |
| 0.7 | 0.5 | 0.4 | 0.3 | 0.1 | 0 | 0 | 0 | 1 | 0 | .00 | .00 | .00 | .99 | .00 |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 | 0 | 1 | .00 | .00 | .00 | .00 | .99 |
| 0.1 | 0.4 | 0.6 | 0.2 | 0.1 | 1 | 0 | 0 | 0 | 0 | .99 | .00 | .00 | .00 | .00 |
| 0.8 | 0.5 | 0.5 | 0.7 | 0.9 | 0 | 1 | 0 | 0 | 0 | .00 | .99 | .00 | .00 | .00 |
| 0.0 | 0.1 | 0.3 | 0.6 | 0.9 | 0 | 0 | 1 | 0 | 0 | .00 | .00 | .99 | .00 | .00 |
| 0.9 | 0.5 | 0.4 | 0.1 | 0.0 | 0 | 0 | 0 | 1 | 0 | .00 | .00 | .00 | .99 | .00 |
| 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0 | 0 | 0 | 0 | 1 | .00 | .00 | .00 | .00 | .99 |
| 0.3 | 0.6 | 0.9 | 0.6 | 0.5 | 1 | 0 | 0 | 0 | 0 | .99 | .00 | .00 | .00 | .00 |
| 0.8 | 0.6 | 0.5 | 0.7 | 0.9 | 0 | 1 | 0 | 0 | 0 | .00 | .99 | .00 | .00 | .00 |
| 0.5 | 0.6 | 0.7 | 0.9 | 1.0 | 0 | 0 | 1 | 0 | 0 | .00 | .00 | .99 | .00 | .00 |
| 0.7 | 0.5 | 0.4 | 0.3 | 0.1 | 0 | 0 | 0 | 1 | 0 | .00 | .00 | .00 | .99 | .00 |
| 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0 | 0 | 0 | 0 | 1 | .00 | .00 | .00 | .00 | .99 |
| inputs | output atteso | output ottenuto | ||||||||||||
| h1 | h2 | h3 | h4 | h5 | M | V | P+ | P- | P0 | m | v | p+ | p- | p0 |
| 0.0 | 0.1 | 0.5 | 0.4 | 0.2 | 1 | 0 | 0 | 0 | 0 | .99 | .00 | .00 | .00 | .00 |
| 0.5 | 0.3 | 0.1 | 0.3 | 0.4 | 0 | 1 | 0 | 0 | 0 | .00 | .98 | .00 | .00 | .03 |
| 0.1 | 0.2 | 0.5 | 0.7 | 0.9 | 0 | 0 | 1 | 0 | 0 | .00 | .00 | .99 | .00 | .00 |
| 0.5 | 0.4 | 0.2 | 0.1 | 0.0 | 0 | 0 | 0 | 1 | 0 | .00 | .00 | .00 | .99 | .00 |
| 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0 | 0 | 0 | 0 | 1 | .00 | .00 | .00 | .00 | .99 |
| 0.3 | 0.4 | 0.5 | 0.3 | 0.2 | 1 | 0 | 0 | 0 | 0 | .99 | .00 | .00 | .00 | .01 |
| 0.6 | 0.4 | 0.1 | 0.3 | 0.8 | 0 | 1 | 0 | 0 | 0 | .00 | .99 | .00 | .00 | .00 |
| 0.4 | 0.5 | 0.6 | 0.7 | 0.9 | 0 | 0 | 1 | 0 | 0 | .00 | .00 | .99 | .00 | .00 |
| 0.4 | 0.3 | 0.2 | 0.1 | 0.0 | 0 | 0 | 0 | 1 | 0 | .00 | .00 | .00 | .98 | .00 |
| 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0 | 0 | 0 | 0 | 1 | .00 | .00 | .00 | .00 | .99 |
| 0.4 | 0.5 | 0.6 | 0.4 | 0.3 | 1 | 0 | 0 | 0 | 0 | .99 | .00 | .00 | .00 | .00 |
| 0.5 | 0.4 | 0.1 | 0.6 | 0.8 | 0 | 1 | 0 | 0 | 0 | .00 | .99 | .00 | .00 | .00 |
| 0.1 | 0.2 | 0.3 | 0.4 | 0.6 | 0 | 0 | 1 | 0 | 0 | .00 | .00 | .99 | .00 | .00 |
| 0.9 | 0.5 | 0.3 | 0.2 | 0.1 | 0 | 0 | 0 | 1 | 0 | .00 | .00 | .00 | .99 | .00 |
| 0.7 | 0.7 | 0.7 | 0.7 | 0.7 | 0 | 0 | 0 | 0 | 1 | .00 | .00 | .00 | .00 | .99 |