f007 Geometria triangolare
Da: ""antonio
david"" <antonio_d_98@hotmail.com>
Data: venerdì 30 giugno 2000 19.03
Il triangolo ABC equilatero di lato L in
figura e' internamente diviso in tre triangoli di lati (30,40,L),
(30,50,L) e (40,50,L) come mostrato in figura
A
/\
/* \
/ * \
/ 30 \
/ * \
/ * * \
/ 40 * \
/ * 50 \
/* * \
B------------------C
Calcolare la lunghezza L del lato, possibilmente senza usare metodi numerici approssimati.
Da: "Silvio Sergio"
<mg9322@mclink.it>
Data: venerdì 30 giugno 2000 16.20
Riporto la dimostrazione, a mio avviso molto bella, data da
Andras Horvath e
presa da http://www.mathcad.com/puzzle.html
********************
Denote the vertices of the triangle on the 30,40 and 50 sections
by A, B and
C resp. and let the meeting point of the sections be P. Rotate
the triangle
around C by 60 degrees clockwise, the new positions of the points
denoted by
A', B', C' and P' resp. Clearly C = C' and A = B'. Since PC and
P'C' = P'C
are two sections of length 50 with an angle of 60 degrees between
them, PCP'
is an equilateral triangle , hence PP' = 50. But then APP' is a
30-40-50
triangle that is known to be right angled , the angle PAP' is 90
degrees.
AP' = B'P' is a 60 degree rotation of BP , thus the angle BPA is
90 + 60 =
150 degrees. Now for AB = x we have the equation:
x^2=30^2+40^2-2*30*40*COS(150)
The solution is x:=10*sqrt(25+12*sqrt(3)) i.e.
x:=67.66432567522307
******************
Da: "Andrea Artesiani"
<overman@libero.it>
Data: venerdì 30 giugno 2000 21.25
Forse c'è un modo più veloce, ma io ho usato questo:
applichiamo il teorema di Carnot ai 3 triangoli e otteniamo:
L^2=30^2+40^2-2*30*40*cosA
L^2=30^2+50^2-2*30*50*cosB
L^2=40^2+50^2-2*40*50*cos(A+B)
l'ultimo coseno sarebbe cos(2pi-A-B) che è uguale a cos(A+B)
sviluppando cos(A+B) in cosAcosB-sqrt(1-cos^2A)*sqrt(1-cos^2B)
troviamo poi il valore di L (lo trova il Derive):
L=sqrt(2500+1200*sqrt(3))
inoltre:
A=150°
B=113.13°
C=96.87°
Da: "Silvio Sergio"
<mg9322@mclink.it>
Data: sabato 1 luglio 2000 19.07
Prendendo spunto dalla soluzione che ho riportato venerdi`, ne ho
elaborata una mia che non fa uso di trigonometria.
Costruiamo tre triangoli equilateri di lato 30, 40 e 50 e
congiungiamo i vertici di questi triangoli con i vertici A, B e
C. La figura ottenuta e` formata da:
1) 3 triangoli equilateri di lato 30, 40 e 50 + 3 triangoli
rettangoli 30-40-50
2) 1 triangolo equilatero ABC + 3 triangoli ACB', BCA', ABC', la
cui area totale eguaglia quella di ABC.
A
_.-'/\-_
_.-' /| \ -_
_.-' / | \ -_
_--' / | \ -_ B'
C'---__ / |30 \_.-'|
\ ---__ / | _.-'\ |
| -/-__ |-' \ |
\ / /\ \ |
| / / | \ \ |
\ /40/ | 50\ \ |
| / / | \ \ |
\ // | \\|
B--------|---------------C
'. | _.--'
'. | _.--'
'. | _.--'
'|'
A'
Eguagliando i due modi di calcolare l'area dell'"esagono" si trova facilmente il lato del triangolo ABC.
f008 Tiangoli e tetraedro
Da: "Paolo Licheri"
<paolo.licheri@tin.it>
Data: martedì 4 luglio 2000 12.45
Dato un triangolo generico, di lati
a,b,c, voglio costruire un tetraedro che abbia le quattro facce
uguali al triangolo dato.
La costruzione e' possibile:
_sempre?
_in alcuni casi?
_mai?
Se possibile solo in alcuni casi, quali sono le condizioni che il
triangolo dato deve rispettare?
Se la costruzione e' possibile, quale sara' il volume del
tetraedro?
Da: "Silvio Sergio"
<mg9322@mclink.it>
Data: martedì 4 luglio 2000 14.43
Secondo me tutti i triangoli acutangoli.
Raddoppia le dimennsioni del triangolo di partenza e unisci i
punti medi:
otterrai lo sviluppo del tetraedro, analogo a quello del
tetraedro regolare.
Esempio:
a/'-_b /____'-_ a/'-_ /'-_b /____'-_/____'-_ c c
Per il volume ci sarà una formula analoga a quella di Erone (?) per il calcolo dell'area dati i lati.
Da: "El Filibustero"
<spalland@comune.re.it>
Data: martedì 4 luglio 2000 15.11
E' possibile per tutti e soli i triangoli acutangoli.
>Se la costruzione e' possibile, quale
sara' il volume del tetraedro?
sqrt(2)/12 * sqrt((aa+bb-cc)(aa-bb+cc)(-aa+bb+cc)). Ciao
Da: "Paolo Licheri"
<paolo.licheri@tin.it>
Data: martedì 4 luglio 2000 17.37
> E' possibile per tutti e soli i
triangoli acutangoli.
Esatto! si puo'dimostrare in questo modo:
. C . /\ . / \ . / \ . / \ . / \ . A /_______________\B . \ / . \ / . \ / . \ / . \ / . \/ . C'
Costruiamo il triangolo ABC', uguale ad ABC (A e' il lato
maggiore), in modo da formare un parallelogramma.
Facciamo ruotare ABC' nello spazio, attorno ad AB, finche' la
distanza CC' sia uguale ad AB.
A questo punto, unendo CC' si ha il tetraedro.
Se l'angolo C e' ottuso, la diagonale CC' del parallelogramma e' inizialmente minore di AB, e diminuisce ancora con la rotazione, quindi non potra' mai uguagliare AB.
Se C e' retto, si ha in partenza CC'=AB, e quindi nel piano si ha un tetraedro degenere, di volume zero
> >Se la costruzione e' possibile,
quale sara' il volume del tetraedro?
> sqrt(2)/12 * sqrt((aa+bb-cc)(aa-bb+cc)(-aa+bb+cc)). Ciao
Per dire il vero, questo non l'avevo calcolato, ma... mi fido.
:-)
f009 CIGM14
Dario:
Sempre dai Campionati dei Giochi Matematici (finali)
questo prob.che e' stato il piu' difficile nessuno lo ha risolto
nei tempi concessi. Ho trovato una sol. che si e' poi rivelata
giusta. Mi sembra un bel problema:
<Qual e' il numero minimo di piani appartenenti a tre
direzioni, che permettono di dividere lo spazio in modo che il
numero delle parti non limitate sia il doppio del numero di
quelle limitate ??>
Paolo:
Non sono sicuro di aver capito bene il testo, perche', se
e' come l'ho interpretato, mi sembra piu' facile di molti altri
che abbiamo gia' visto. Ho interpretato *piani appartenenti a tre
direzioni* come piani paralleli a tre piani dati, per esempio
piani orizzontali, verticali diretti Nord-Sud, e verticali
diretti Est-Ovest (o altre tre giaciture non necessariamente
perpendicolari tra loro).
Se e' cosi', siano A,B,C i numeri dei piani nelle tre direzioni.
Lo spazio viene suddiviso in
(A+1)*(B+1)*(C+1) parti complessive
delle quali
(A-1)*(B-1)*(C-1) sono limitate.
Dovra' essere:
(A+1)*(B+1)*(C+1)=3*(A-1)*(B-1)*(C-1)
da cui, per ogni coppia A,B, resta determinato
C=(4*A*B-2*A-2*B+4)/(2*A*B-4*A-4*B+2)
Costruisco una matrice, dove le intestazioni di riga e colonna
sono i possibili valori interi di A e di B, e agli incroci
calcolo C con la formula sopra scritta.
Tra i valori di C interi, trovo il minimo:
A+B+C=5+5+7=17
altri valori
4+6+8=18
4+5+11=20
3+9+11=23
3+8+13=24
ecc.
Naturalmente ho usato un foglio elettronico (non so se ai
Campionati dei Giochi Matematici fosse consentito).
fammi sapere se ho visto giusto
Dario:
Bene Paolo, la risposta e' esatta!. Purtroppo oltre al
poco tempo.. solo carta e matita. Nemmeno una misera calcolatrice
tascabile.
Silvio:
Io l'avevo affrontato senza computer (Paolo ovviamente mi
aveva preceduto) e avevo trovato (abbastanza in fretta per la
verita') la formula
(A+1)*(B+1)*(C+1)=3*(A-1)*(B-1)*(C-1) di Paolo che avevo scritto
3xyz=(x+2)(y+2)(z+2) con x<=y<=z. Poi avevo pensato che
l'unico modo di fattorizzare diversamente 3xyz sarebbe stato
accorpando il 3 col minore del primo membro per farlo diventare
il maggiore del secondo membro, per cui x+2=y, y+2=z e z+2=3x
cioe' z+2 multiplo di 3.
Si possono scartare facilmente z=1 e z=4, e quindi si trova z=7 e
dunque y=5 e x=3, ovvero A,B,C=4,6,8 con 18 piani in totale.
Ma Paolo ovviamente ha fatto meglio, ed e' risultato che il
fattore 3 viene distribuito su tutti i tre fattori (esistono
altri numeri oltre gli interi, pare). Perche' ho postato una
soluzione in ritardo e perdipiu' sbagliata? Solo per avvalorare
cio' che dice Dario: purtroppo, in poco tempo e con carta e
matita non e' che si possono fare i miracoli, e qui servivano
dieci minuti solo per capire cosa chiedeva il quesito.
f013 Cerchi di Ford
Silvio
Sulla retta reale, sopra il
punto 1/2 (cioe' tangente la retta nel punto 1/2) disegniamo un
cerchio di diametro 1/4. Sopra il punto 2/3 disegniamo un cerchio
di diametro 1/9.
I due cerchi sono tangenti (controllare...). Incastriamo un
cerchio tra i due e la retta. In che punto sara' tangente alla
retta?
Generalizzare per due cerchi tangenti in a/c (diametro 1/c^2) e
b/d (diametro 1/d^2), con a*d e b*c interi consecutivi.
Stefano
se non ho sbagliato i conti...
Il punto in cui il terzo cerchio è tangente
alla retta è "m/n" con "n=c+d" ed
"m=(an+1)/c" (che *dovrebbe* essere intero).
La relazione tra il primo (a/c) ed il secondo (b/d) è "a/c
= b/d - 1/cd" La stessa vale tra il primo ed il terzo:
"a/c = m/n - 1/cn" Mentre tra il terzo ed il secondo
è: "m/n = b/d - 1/nd"
Risolvendo due di queste nella terza si ottiene "n=c+d"
e ponendo questa nella seconda (ad es.) si ottiene la relazione
su "m".
Ci si potrebbe costruire un frattale, vero?
Silvio
E' giusto, ma m si puo' semplificare ancora....
Stefano
>E' giusto, ma m si puo'
semplificare ancora....
Già, già ^____^;;;
(a(c+d)+1)/c = (ac+ad+1)/c = (ac+(bc-1)+1)/c = a+b
Silvio
Esatto.
Quindi per trovare un nuovo punto tra due dati basta sommare
numeratori e denominatori!
Per esempio, tra 1/2 e 2/3 ci sara' un cerchio sopra al punto
(1+2)/(2+3)=3/5.
Si puo' infittire a piacimento con estrema facilita'.
f014 L'esagono
Livio Zucca
Questo e' un esagono equilatero ma non regolare: di lato 5, ha la chiave verticale di 8, cosi' potete disegnarlo sulla carta quadrettata. E simmetrico sui due assi.
_________ ________
/ \ |
/ \ |
/ \ |
/ | \ |
/ ___|___ \ |
\ | / |8
\ | / |
\ / |
\ / |
\_________/ ______|_
5
Il problema e' suddividerlo in triangoli rigorosamente simili tra di loro. Nessun trucco. Vince chi usa il minor numero di triangoli. OK?
Paolo Licheri
Ho trovato una soluzione con 14 triangoli. Sono troppi?
Con due segmenti verticali divido la figura in due triangoli
isosceli di lati 8,5,5, ed un rettangolo 8*5.
Tracciando le altezze divido ciascun triangolo isoscele in due
triangoli rettangoli di lati 3,4,5.
Divido poi il rettangolo in due rettangoli, rispettivamente 8*3
ed 8*2.
Divido il rettangolo maggiore in due 4*3, ed il minore in tre
(8/3)*2.
Noto che tutti questi rettangoli hanno i lati in proporzione 4/3,
quindi tracciando le diagonali, li divido in triangoli rettangoli
simili ai primi.
Livio
Carina, cosi' lineare che non l'avevo vista. Penso cmq che si possa fare di piu' :o)
Paolo
Sono arrivato a 13, sempre triangoli rettangoli con i lati in rapporto 3/4/5; e' un po' complicato da descrivere puoi vederlo qui

Livio
Hai presente un minimo relativo, detto anche cul de sac? Ecco, tu sei li'! :o)
Paolo
E' vero, mi ostinavo a cercare soluzioni grafiche, simmetrie,
triangoli pitagorici ecc.
Invece si può risolvere analiticamente. Si può arrivare a 6
triangoli.
Con la diagonale orizzontale divido l'esagono in due trapezi
isosceli, con base maggiore 11 e gli altri tre lati 5.
Divido ciascun trapezio in tre triangoli in questo modo: cerco
sulla base maggiore un punto P, distante X da un estremo, tale
che sia: X:5 = 5:(11-X) quindi unisco P con gli altri due vertici
del trapezio.
Si può verificare facilmente che i tre triangoli sono simili; in
particolare hanno rispettivamente il lato maggiore, quello
intermedio ed il minore lunghi 5.
Livio
Spero che trovare questa soluzione ti abbia dato la stessa
gioia che ha dato a me pensarla. E' da un po' che ci lavoravo.
Penso proprio che sia inedita, 'sta volta. Quando l'ho vista non
mi sembrava vero. L'ho verificata n volte prima di postarla.
Unico rincrescimento e' che ci sei arrivato troppo in fretta
(l'ho sempre detto che in questo NG ci sono troppi geni!).
Ci sono almeno due altri insidiosi cul de sac grafici: - essendo
arctan(4/3)=2*arctan(1/2), la figura e' scomponibile in 13 DOMs
(DOM = 1/2 Domino) - per la stessa magia, possiamo scomporre
l'esagono in 11 triangoli isosceli non facili da scovare.
f015 Piastrelle di due misure
Silvio Sergio
Dobbiamo riempire una stanza quadrata utilizzando due soli tipi di piastrelle più piccole, quadrate a loro volta, di misure diverse. Di ciascuno tipo ne possiamo usare sei. Non sono ammesse sovrapposizioni o sconfinamenti. Qual è la massima porzione copribile?
A scanso di equivoci: con 7 per tipo potremmo coprire un'area di 36/37 in questo modo:
___ ___ _ | | |_|_ |___|___|_|_| | | |_|_| |___|___|_|_| | | | | |___|___|___|
Paolo Licheri
Inizio con una soluzione banale, e poi con un lievissimo
miglioramento (che sicuramente non rappresenta ancora il
ricoprimento ottimale).
Per comodità considero fisso, pari a 2 unità, il lato della
piastrella grande, e variabili il lato della stanza e quello
della piastrella piccola.
La prima soluzione che viene in mente è quella di disporre le
piastrelle grandi secondo un rettangolo 6*4 oppure a scaletta, e
completare con sei piastrelle piccole di lato 1 variamente
disposte, per esempio come nel disegno seguente; il ricoprimento
risulta
30/36 = 0.8(3)
. ___ _ _ _ _ . | |_|_|_|_| . |___|_|_| . | | | . |___|___|___ . | | | | . |___|___|___|
Alcune considerazioni mi portano a ritenere che questo sia il
ricoprimento massimo se si dispongono tutte le piastrelle con i
lati paralleli a quelli della stanza.
Provo allora a disporre le sei piastrelle grandi, e cinque
piastrelle 1*1, in questo modo:
. ___ ___ _ . | |_|_| |_| . |___|___ _ . | | | |_| . |___|___|_|_| . | | | | . |___|___|___|
piazzo poi la sesta piastrella piccola inclinata di 45 gradi,
in modo che la metà di un lato cada sul vertice della piastrella
grande centrale.
Vedo che la sesta piastrella piccola non tocca i vertici delle
altre tre che le stanno intorno; provo quindi a dilatare tutte le
piastrelle piccole in modo da recuperare il gap.
Non ho voglia di cercare analiticamente la misura ottimale,
graficamente trovo la soluzione con piastrelle piccole di lato
1.07 (o poco più) e area 1.1449.
Il ricoprimento risulta 30.8694/36 = 0.8548..., migliore, se pure
di pochissimo, del precedente.
Paolo Licheri
Ancora un piccolo miglioramento:
. ___ _ . | |_ |_| . |___|_|_ . | | |_ . |___|___|_|_ . | | | | . |___|___|___|
Sempre in una stanza 6*6, sei piastrelle grandi di lato 2 e
tre piastrelle di lato 1.083, disposte come in figura.
Nello spazio vuoto ci sta una fila, inclinata di 45 gradi, con le
altre tre piastrelle da 1.083.
Il ricoprimento risulta 0.862...
Silvio Sergio
Non credo che nessuno sia riuscito a fare di meglio.
Per una panoramica dei migliori risultati raggiunti con n + m
piastrelle (n,m<=17) vedi
http://www.stetson.edu/~efriedma/mathmagic/0400.html
f016 Pentagono
Dario Uri
ABCDE e' un pentagono convesso i cui
lati misurano 1,2,3,4,5, ma non necessariamente in questo ordine.
Diciamo che F,G,H,I sono i quattro punti di mezzo dei lati
AB,BC,CD,DE rispettivamente.
X e' il punto di mezzo del segmento FH, e Y e' il punto di mezzo
del segmento GI.
Se la lunghezza del segmento XY e' un intero, quanto misura il
lato AE ?
Livio Zucca
QUATTRO (!)
> Mi piacerebbe sapere come hai fatto. (Brute Force?)
Fortuna, solo fortuna!
Incomincio distrattamente a mettere su un cad il tuo pentagono, e dato che son pigro, scelgo la strada piu' semplice:
_____5____
| \2
1| /
|_________/3
4
con 4 perpendicolare a 1 perpendicolare a 5: BINGO!
Gia' avevo subdorato che XY intero dovesse essere =1, faccio una
rapida verifica su alcune altre combinazioni e mi convinco che e'
la giusta risposta, solo perche' esiste il quesito. Ho visto che
sarebbe un altro paio di maniche fare una dimostrazione per
benino. :o)
SuperPollo
M'e' piaciuta tantissimo la soluzione di Livio [fortunosa quanto si vuole, ma certo simpatica], ma vorrei proporne una piu' geometrica
Prima di tutto, chiamo E' e A' i punti X e Y. Chiamo L il
punto medio di EA. E di seguito:
B' il punto medio di GL,
C' il punto medio di FI,
D' il punto medio di HL.
Ottengo il pentagono A'B'C'D'E'.
Ad occhio questo pentagono e' simile all'originale, ed ogni suo
lato e' 1/4 del corrispondente lato del pentagono ABCDE.
Una traccia [o uno straccio] di dimostrazione [che non ho seguito
fino in fondo, ma sono pronto a scommettere che possa portare al
risultato] e'...
Il segmento GF e' parallelo alla diagonale AC, e lungo la meta'.
A'C' e' parallelo a GF [e quindi ad AC] e lungo la meta' [quindi
1/4 di AC].
E questo vale per tutte le diagonali dei due pentagoni.
Senza approfondire troppo mi pare sufficiente per rispondere...
quattro
[l'unico divisibile per quattro ;-)].
Livio
Per farmi perdonare la soluzione fortunosa, metto giu' qua la
dimostrazione che XY vale sempre AE/4, per qualunque pentagono,
anche concavo.
(Adesso e' facile).
C
/ '.
/ '. H
/ '*
G* '.
/ '.
/ /D
B/ X*-*Y /
\ /
\ * I
F * /
\ /
\______/
A E
Impongo queste coordinate cartesiane:
P(A)=0,0
P(B)=x2,y2
P(C)=x3,y3
P(D)=x4,y4
P(E)=x5,0
Da cui ricavo i punti mediani F,G,H,I:
P(F)=x2/2,y2/2
P(G)=(x2+x3)/2,(y2+y3)/2
P(H)=(x3+x4)/2,(y3+y4)/2
P(I)=(x4+x5)/2,y4/2
e i mediani dei mediani:
P(X)=(x2+x3+x4)/4,(y2+y3+y4)/4
P(Y)=(x2+x3+x4+x5)/4,(y2,y3,y4)/4
da cui risulta:
y(X)=y(Y) cioe' XY sempre parallelo ad AE
XY=x(Y)-x(X)=x5/4=AE/4
c.v.d. :o)
Andrea Artesiani
AE vale 4.
Dopo un po' di sostituzioni si trova
XY=AE/4, dovendo essere intero, con 1<=AE<=5
l'unica possibilità e AE=4
f017 Golden ratio
Livio Zucca
Ho tre tavolette quadrate unitarie.
Taglio ciascuna in due parti, con un taglio a piacere, anche non
rettilineo. Con i pezzi compongo un quadrato pieno di lato L. Si
puo' buttare via un pezzo.
Esempio:
___ ___ ___ |___| |___| | |_| |___| |___| |___| 1 ___ _ |___| | _ |___|_| | |_ |___|_| L e butto: |___| 1/L = 2/3
Se usassi tutto il materiale varrebbe 1/L=1/SQR(3)
Vince chi si avvicina di piu' al rapporto aureo (!)
Dario Uri
Dato che 809/500 = 1.618 ~fi
Metto le tavolette con lato 500 ed il quadrato grande con lato
809.
La costruzione diventa semplice es:
_______________ | | | | | A ______| | | | | | | | | C |B | |__|______ __|__| | | | | B | A | |_________|_____|
Dalla prima tavoletta A = 500x500 seziono un quadrato piu'
piccolo 309x309
La seconda tavoletta B, e' divisa in 2 pezzi 500x309 e 500x191.
Il pezzo C coi lati 118,500,427,309,309,191 e' la parte
utilizzata della terza tavoletta.
Paolo Licheri
Sia 1+x il lato del quadrato richiesto, con x=0.618...
Mi pare che si possa approssimare a piacere, ed anche trovare la soluzione esatta, sempre che si sia in grado di costruire un segmento lungo x (non ricordo, ma mi pare che esista un metodo grafico per farlo)
Divido il primo quadrato in due strisce A1, A2, larghe rispettivamente x, 1-x
._ _ _ _ _. | | | | | | | A1 |A2 | | | | |_ _ _|_ _|
Ritaglio dal secondo un rettangolo B2 di lati x, 1-x
._ _ _ _ _. | | | | |B2 | | B1 |_ _| | | |_ _ _ _ _|
Unisco i quattro pezzi come in figura, su un quadrato di lato 1+x:
._ _ _ _ _ _ _ _. | | | | A1 | C | |_ _ _ _ _| | | |_ _ _ _ _| | | A2 | | B1 |_ _ _ _ _| | | B2 | |_ _ _ _ _|_ _ _|
rimane un'area C non coperta, a forma di L, con entrambi i lati non maggiori di 1
Sovrappongo il terzo quadrato all'area C, con un vertice in corrispondenza del vertice della L, e ritaglio via la parte eccedente
Livio Zucca
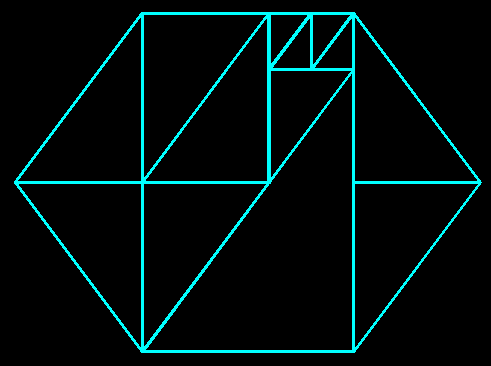
Per finire una soluzione esatta che ricorda quelladissezione del rettangolo proposta tempo fa da Dario Uri:
___________ |\ | | \ | | \ | | \ |1 | \ | | T \ | |______\____|_ _ _ _ | \ | | | \ | | | \ | | |1 \| | | \ | | |\ | |___________| \ |L | | \ | | | \ | | | \ | |1 | T \ | |___________|______\| | scarto | |___________|x
L^2 = (2-x)^2 = 3-x
Lo stupore e' che il taglio orizzontale del triangolo T
coincida, per la soluzione mat. esatta, con la separazione dei
primi due quadrati.
E questa e' l'unica soluzione a tagli rettilinei che abbia
trovato, mentre la sol.nr.2 e' quella con il quadrato complessivo
relativamente piu' grande.
f018 Triangolazioni naturali
Dario
Il mio amico argentino Rodolfo Kurchan
propone il seguente problema.
I numeri triangolari possono essere rappresentati come
rettangoli:
1+2+3 = 2x3
1+2+3+4 = 2x5
1+2+3+4+5 = 3x5
1+2+3+4+5+6 = 3x7
1+2+3+4+5+6+7 = 4x7, 2x14
1+2+3+4+5+6+7+8 = 6x6, 2x18, 3x12, 4x9
1+2+3+4+5+6+7+8+9 = 5x9, 3x15
1+2+3+4+5+6+7+8+9+10 = 5x11
......ecc....
Il problema allora, e' quello geometrico di dividere i rettangoli, con linee congiungenti coordinate intere del reticolo, in modo da ottenere n triangoli con aree di 1,2,3,...,n rispettivamente.
Es. di soluzioni:
___b_______c | | | | |___|___|___| | | | | |___|___|___| a
2x3, tracciando le linee ab, ac, si ottengono 3 triangoli appunto di aree 1,2,3.
a __b_______________
| | | | | |
|___|___|___|___|___|
| | | | | |
|___|___|___|___|___|
c d
2x5, tracciando le linee ac, cb, bd, si ottengono 4 triangoli di area 1,2,3,4 rispettivamente.
Per quali altri rettangoli elencati
sopra esiste almeno una soluzione ?
Attualmente ho risultati riguardanti 2x3,2x5,4x7,6x6,4x9.
Paolo Licheri
Per ora solo un risultato parziale:
Esiste almeno una soluzione per tutti i casi in cui n sia multiplo di 4.
Disegno un rettangolo base n+1, altezza n/2
con linee orizzontali lo divido in n/4 rettangoli di altezza 2
traccio una diagonale di ciascun rettangolo, e ottengo n/2
triangoli, base n+1, altezza 2
su ciascun triangolo cerco un punto opportuno sulla base, in modo
da dividerla in due parti
n,1: n-1,2; n-2,3 ecc.
e unendo questi punti con i vertici dei rispettivi triangoli,
ottengo gli n triangoli cercati.
Analogamente, se n==3(mod4)
risulta (n+1) multiplo di 4
traccio il primo rettangolo base n, altezza (n+1)/2 e procedo
come sopra
__________________
Posso anche scomporre le figure precedenti, disponendo in orizzontale tutti i rettangoli che erano sovrapposti, ottenendo un rettangolo di altezza 2 e lunghezza quanto basta.
Quindi nei due casi
n==3(mod 4)
e
n==0(mod 4)
la suddivisione è sempre possibile con un rettangolo 2 *
(n*(n+1)/2)
Livio Zucca
Mi sembra di poter dimostrare che i rettangoli dispari_X_dispari non abbiano soluzione.
La mia congettura e' che tutti i rettangoli dispari x dispari non abbiano soluzione. Non sono riuscito a produrre una vera e propria dimostrazione, ma solo una serie di verifiche a prova della congettura.
Il primo passo e' dire che il problema non ha soluzioni se non e' possibile scomporre unn rettangolo dispari x dispari in triangoli con area intera e vertici sul reticolo degli interi.
Un triangolo con vertici sul reticolo degli interi e la base sul perimetro del rettagolo avra' area intera solo se almeno la base o l'altezza e' pari (base x altezza / 2 = intero).
Ora mi riferisco a questo .gif in rete:
http://members.theglobe.com/liviozucca/images/rodolfo.gif
La Fig.1
mostra che non c'e' soluzione se si prendono i vertici solo sul
perimetro del rettangolo:
poiche' le altezze sono dispari, le basi devono essere tutte
pari, ma la somma di segmenti pari non puo' dare un lato dispari.
La Fig.2 mostra che non c'e' soluzione con un vertice interno:
il punto 'A' puo' avere una distanza pari solo da due lati.
Verso gli altri due lati si possono fare solo triangoli interi
con basi pari, ma si finisce sempre per avere un resto dispari. A
nulla serve 'smussare' l'angolo con triangoli
interi (linea blu) che dovranno avere almeno un lato pari e
produrranno almeno un resto dispari.
La Fig.3 mostra che non c'e' soluzione con 2 vertici interni, ciascuno a distanza pari da due lati distinti: allora il segmento AB sara' la diagonale di un rettangolo dispari e qualunque spezzata che lo comprenda e che unisca due lati opposti (linea rossa) separa il rettangolo in due figure ad area non intera, non scomponibile ovviamente in triangoli ad area intera. (I triangoli rosa non sono interi. ABC si puo' verificare sottraendo al rettangolo circoscritto i triangoli verdi interi e quello azzurro non intero).
La Fig.4 mostra che e' possibile arere un triangolo intero a lati obliqui inscritto in un rettangolo dispari. Si potrebbe pensare di usare questo per risolvere il problema, ma la Fig.5 mostra che non e' possibile perche' c'e' sempre almeno una spezzata (linea rossa) che unisce due lati opposti e separa il rettangolo in due aree non intere.
Mi manca una generalizzazione che forse puo' raggiungere una mente piu' matematica della mia. Comunque penso che ogni rettangolo specifico sufficientemente piccolo possa avere una dimostrazione del genere.
Livio
Altra cosa invece sarebbero i triangoli... triangolari.
E sono simpatici, perche' assumono la forma del calcolo n(n+1)/2.
Questi, ad esempio diventano scomponibili:
1+2+3+4+5 = 5x6/2
1+2+3+4+5+6+7+8+9+10 = 10x11/2
Anche gradevoli. Facili ma non banali.
Forse tutti. Provare per credere!
Paolo
Tutti i numeri triangolari, sì; tutti i triangoli, credo di
no, devo verificare.
La distinzione dipende dal fatto che ciascun numero triangolare
può generare infiniti triangoli di uguale area.
Per esempio, data la base AB, di lunghezza n, sull'asse x, il
terzo vertice C può essere uno degli infiniti punti di ascissa
intera ed ordinata n+1.
Se anche ci volessimo limitare a triangoli rettangoli, da ogni
numero triangolare se ne possono ottenere almeno due:
il primo con cateti n, (n+1) e l'altro con cateti n/2, 2*(n+1),
oppure 2*n, (n+1)/2 a seconda che n sia pari o dispari.
Se ci limitiamo ulteriormente, considerando solo il primo caso (cateti n, n+1), effettivamente esiste sempre la soluzione:
in coordinate cartesiane, senza staccare la penna dal foglio,
traccio la spezzata
0,1 0,0 2,0 0,1
0,3 2,0
4,0 0,3
0,5 4,0
ecc.
f020 Piramidi e arance
Alla festa dell'agrumeto, i ragazzi del
paese dopo diverse prove, sono riusciti a sistemare tutte le 8500
arance del raccolto in una piramide, che ora e' in bella vista
nella piazza del paese.
Come sara' fatta questa piramide ??
============================
Massimiliano
Aracione
============================
Matteo Frigerio
La classica disposizione tetraedrica fallisce. La disposizione
ottaedrica (a base quadrata) pure. Prendiamo pero' come base un
rettangolo di a*b arance, costruiamo sopra un piano di
(a-1)*(b-1) arance e cosi' via, fino ad avere, se a>b,
(a-b-1)*1.
Per avere 8500 arance la base della piramide puo' essere
36*24, 568*5, 851*4, 2834*2.
Posso prendere un'arancia?
Certo!
Mi piace quella li' in basso...
Nooo!
=======================
Paolo Licheri
29^2+28^2+27^2+.......+6^2=8500
in realta' e' un tronco di piramide
24 piani quadrati
base inferiore 29*29
base superiore 6*6
peccato che non ci fossero altre 55 arance, si sarebbe potuta
costruire una vera piramide a punta
29^2+28^2+27^2+.......+1^2=8555
==============================
Vacirca Domenico
Potrebbe essere una piramide tronca a base quadrata con 29
arance per lato alla base e 6 arance per lato in cima.
============================
Dario Uri
Volevi dire (a-b+1)*1
Difatti, la piramide era intesa completa, non tronca, le prime 3
soluzioni sono possibili, ma l'arancia che ti sei mangiato,
provenive dalla quarta:
2834*2+2833*1=8501.
La 24*36 con in cima una fila di 13 arance e' senz'altro la piu'
estetica, ed e' quella scelta dai ragazzi, che per sicurazza
hanno piazzato attorno alla base una cornice di legno.
Mi sono divertito ad elaborare una formuletta che restituisce
il numero totale delle palle presenti in una piramide
rettangolare in funzione di n = numero palle della prima fila in
alto n*1 e p = numero dei piani (strati).
Se ci volete provare.