6.2  L'azione efficace a bassa energia

Nel seguito, considereremo una azione efficace quadridimensionale a bassa energia ricavata dalla teoria della corda eterotica [38]; essa tiene conto dell'accoppiamento non minimale alla gravità di un campo di modulo, dovuto ad effetti di soglia ad un ``loop''; in unità di misura in cui $c = \hbar = G = 1$, essa è data da:

$$I = \frac{1}{16 \pi} \int d^4x \sqrt{-g} \, e^{-2 \phi}\lef......\left(\phi -\frac{q}{3}\psi\right)}\right) F^2 \right] \: ,$$ (6.1)

 

dove $\phi$ è il dilatone; $\psi$ è il compattone ottenuto dalla riduzione dimensionale della teoria in dieci dimensioni; g è il determinante del tensore metrico; R è lo scalare di curvatura; $F^2 = F_{\mu \nu} F^{\mu \nu}$, dove $F_{\mu \nu} = \partial_{\mu} A_{\nu} -\partial_{\nu} A_{\mu}$è il tensore di campo elettromagnetico di Maxwell; infine q è una costante di accoppiamento che, in principio, può essere determinata da calcoli a un ``loop''.

L'azione considerata è fondamentale nell'ambito della teoria efficace delle corde in quanto, a partire da questa, è possibile utilizzare le ordinarie tecniche utilizzate in teoria dei campi, per ricavare soluzioni esatte di buchi neri. Soluzioni esatte possono essere ottenute se l'azione viene semplificata tramite l'ansatz:

$$e^{-2\phi} = \frac{q^2}{3}e^{-\frac{2}{3}q \psi} \; ,$$ (6.2)

 

che equivale a porre:

$$\psi = \frac{3}{q} \phi + cost. \; .$$ (6.3)

 

Perciò:

$$\nabla \psi = \frac{3}{q} \nabla \phi\;\;\;\;\; \Leftrighta......;\;\;\;\;(\nabla \psi)^2 = \frac{9}{q^2} (\nabla \phi)^2 \; .$$ (6.4)

 

Dunque, l'azione efficace considerata si riduce a:

$$I = \frac{1}{16 \pi} \int d^4x \sqrt{-g} \, e^{-2 \phi}\lef......la \phi)^2 -\left( 1 +\frac{3}{q^2} \right) F^2 \right] \; .$$ (6.5)

 

Introduciamo a questo punto una nuova costante k, che parametrizza la teoria:

$$k = \frac{3 - 2 q^2}{3 + 2 q^2} \; ,$$ (6.6)

 

ed esplicitiamo rispetto alla costante di accoppiamento q:

$$q = \sqrt{\frac{3}{2} \, \frac{1-k}{1+k}}\;\;\;\;\;\;\;( -1 \leq k \leq 1 ) \; .$$ (6.7)

 

Con questa sostituzione, l'azione si semplifica nella forma finale:

$$I = \frac{1}{16 \pi} \int d^4x \sqrt{-g} \, e^{-2 \phi}\lef......8k}{1-k} ( \nabla \phi )^2 -\frac{3+k}{1-k} F^2 \right] \; .$$ (6.8)

   

Figura 6.1: La funzione di accoppiamento q(k).

 

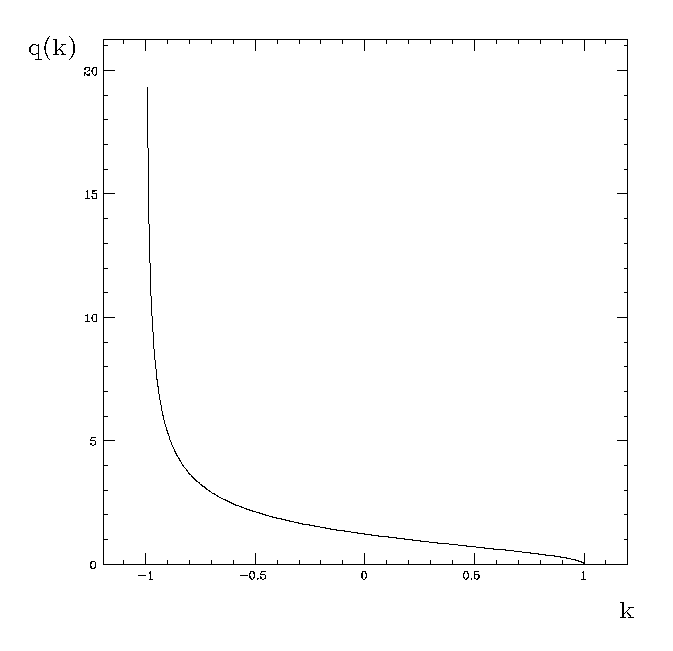
Si noti il particolare andamento della funzione q(k): nel limite singolare per k=1 è q=0; il dilatone si disaccoppia e ci si riconduce alla teoria di Einstein-Maxwell. Nel limite per k=-1, si ha che $q \to \infty$ e l'azione si riduce all'azione delle corde standard in assenza dell'accoppiamento del modulo; questa situazione corrisponde alla soluzione ricavata da Garfinkle, Horowitz e Strominger (soluzioni GHS) [40]. Da notare che, in questo limite, nonostante l'assenza del compattone, è sempre presente il dilatone che, in tale modello, cambia drasticamente molte proprietà dei buchi neri rispetto a quelli di Reissner-Nordström.

 
1999-03-18