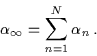| ds2 | = | (6.34) | |
| = | (6.35) | ||
| Fij | = | 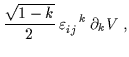 |
(6.36) |
| ds2 | = | (6.34) | |
| = | (6.35) | ||
| Fij | = | 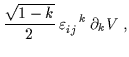 |
(6.36) |
dove:
e:
rappresenta il vettore posizione di un generico punto della sezione spaziale, e si cercano le condizioni che deve soddisfare V per risolvere le equazioni di campo.
L'equazione (6.12.a):
è banalmente soddisfatta per la antisimmetria del tensore ![]() .
.
La verifica della seconda equazione (6.12.b):
è più laboriosa, in quanto bisogna calcolare le quantità ![]() ,
, ![]() ,
F2 ed R; si ha:
,
F2 ed R; si ha:
| |
= | ||
| = | 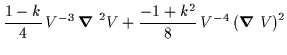 |
(6.37) | |
| = | |||
| = | 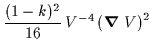 |
(6.38) | |
| F2 | = | ||
| = | 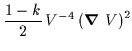 |
(6.39) | |
| R | = | ||
| = | 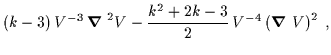 |
(6.40) |
dove l'operatore ![]() è il gradiente nello spazio piatto 3-dimensionale. Sostituendo nella
equazione di campo, si ha che questa è identicamente soddisfatta
se:
è il gradiente nello spazio piatto 3-dimensionale. Sostituendo nella
equazione di campo, si ha che questa è identicamente soddisfatta
se:
| (6.41) |
Analogamente si prova che l'ansatz scelto verifica anche la terza equazione di campo (6.12.c):
La condizione ![]() è, come è noto, l'equazione di Laplace dell'elettrostatica
e della teoria gravitazionale node0.oniana, ed esprime in forma locale
le proprietà dello spazio in cui non sono presenti cariche o masse.
è, come è noto, l'equazione di Laplace dell'elettrostatica
e della teoria gravitazionale node0.oniana, ed esprime in forma locale
le proprietà dello spazio in cui non sono presenti cariche o masse.
Si può scegliere per V una espressione che, in generale, nel caso di una soluzione per buchi neri multipli, sia del tipo:
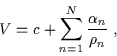 |
(6.42) |
dove ![]() ,
con
,
con ![]() che denota la posizione dell'nmo buco nero.
che denota la posizione dell'nmo buco nero.
V soddisfa l'equazione di Laplace in tutti i punti tranne ![]() ,
dove è singolare, e corrisponde ad una distribuzione di cariche
puntiformi. Quando x si avvicina ad un particolare punto, diciamo
il jmo, il corrispondente termine nella somma domina,
cosicché:
,
dove è singolare, e corrisponde ad una distribuzione di cariche
puntiformi. Quando x si avvicina ad un particolare punto, diciamo
il jmo, il corrispondente termine nella somma domina,
cosicché:
Per c = 1 si ha l'estensione ad N buchi neri del caso
già discusso, per cui la metrica è del tipo di Bertotti-Robinson
vicino all'orizzonte ![]() di
ciascuno dei buchi neri, e tende asintoticamente alla metrica di Minkowski
all'infinito. Come dimostreremo esplicitamente per la metrica ``canonica'',
questa soluzione corrisponde a N masse in cui gravità, elettromagnetismo
e forze scalari si equilibrano in uno spazio asintoticamente piatto.
di
ciascuno dei buchi neri, e tende asintoticamente alla metrica di Minkowski
all'infinito. Come dimostreremo esplicitamente per la metrica ``canonica'',
questa soluzione corrisponde a N masse in cui gravità, elettromagnetismo
e forze scalari si equilibrano in uno spazio asintoticamente piatto.
Per c = 0 invece, si ottiene una soluzione che, in prossimità del jmo termine, è:
e rappresenta ancora uno spazio di Bertotti-Robinson, ma in questo caso la soluzione è di Bertotti-Robinson anche all'infinito, con:
dove: