6.4  Il buco nero estremo

Di particolare interesse sono le soluzioni che corrispondono ad un buco nero dilatonico estremo; questo è il caso limite in cui $r_+ = r_- = \alpha$. Infatti, in questo limite, la temperatura tende a zero, e il buco nero può essere considerato lo stato fondamentale nel processo di evaporazione di Hawking. In questo limite:

$$- \left(1-\frac{\alpha}{r}\right)^{1+k} dt^2 +\left(1-\frac{\alpha}{r}\right)^{-2} dr^2$$               ds² =

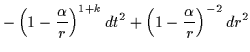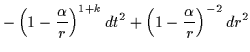$$+ r^2 \left(d\vartheta^2 + \sin^2 \vartheta \,d\varphi^2 \right) \; .$$ (6.20)

 

Posto $r = \rho + \alpha$, si ha infine la forma conforme dell'elemento di linea:

 

$$- \left(1+\frac{\alpha}{\rho}\right)^{-(1+k)} \!\!\!dt^2 +\left(......+ (\rho + \alpha)^2\left(d\vartheta^2 + \sin^2 \vartheta \, d\varphi^2 \right)$$        ds² =

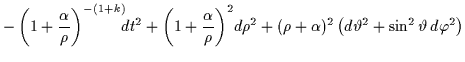$$- \left(1+\frac{\alpha}{\rho}\right)^{-(1+k)} \!\!\!dt^2 +\left(......\rho^2 \left(d\vartheta^2 + \sin^2 \vartheta \, d\varphi^2\right)\right] \; .$$ = (6.21)

 

Inoltre, nel caso estremo, il campo dilatonico è dato da:

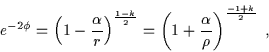$$e^{-2\phi} = \left( 1- \frac{\alpha}{r} \right)^{\frac{1-k}{2}}= \left( 1+ \frac{\alpha}{\rho} \right)^{\frac{-1+k}{2}} \; ,$$ (6.22)

 

e il tensore di Maxwell da:

$$F_{ij} = \frac{\sqrt{1-k}}{2} \,\frac{\alpha}{(\rho + \alph......n_{ij}\;\;\;\;\;\;\;\;\; \left( i,j = (2,3) \, \right) \; .$$ (6.23)

 

Nel limite $k \to 1$, la soluzione si riduce a quella di Reissner-Nordström (normalizzando opportunamente $F_{\mu \nu}$).

Le possibili singolarità per questa metrica si hanno per $\rho = 0$ e $\rho = - \alpha$ (che corrispondono rispettivamente a $r = \alpha$ e r =0). Tuttavia, si noti che per $-\alpha < \rho < 0$ la componente della metrica g₀₀ e il campo dilatonico $\phi$ diventano complessi [41], tranne nei casi in cui k è intero, per cui la soluzione non è prolungabile oltre l'orizzonte.

Un primo metodo per calcolare le singolarità per questa metrica è di vedere il comportamento dello scalare di curvatura. Si ha che :

$$R = - \frac{k^2+2k-3}{2} \,\frac{\alpha^2}{(\rho + \alpha)^2} \; ,$$ (6.24)

 

per cui in prossimità della superficie $\rho = 0$ troviamo:

$$\lim_{\rho \to 0} R = - \frac{k^2+2k-3}{2} \; ;$$ (6.25)

 

pertanto R è regolare e positivo per tutti i valori di k compresi nell'intervallo $-1 \le k < 1$, e si annulla per k = 1.

Per completezza osserviamo che, in prossimità di $\rho = - \alpha$:

$$\lim_{\rho \to -\alpha} R = \infty \; ;$$ (6.26)

 

quindi, per tutti i valori di k, R presenta una vera singolarità in $\rho = - \alpha$.

Per meglio comprendere la natura della superficie $\rho = 0$in cui c'è una singolarità di coordinate, calcoliamo la geodetica ``space-like'' da un punto $\rho_0 > 0$ a tale superficie; si ha:

$$\int_{l(\rho_0)}^{l(0)} dl = \int_{\rho_0}^0\left( 1 + \fr......m} \rho + \alpha \ln \rho \right]_{\rho_0}^0\to \infty \; ;$$ (6.27)

 

per $\rho = 0$ si ha quindi un orizzonte regolare posto a distanza spaziale infinita per tutti i valori di k.

 

Figura 6.2: Sezione spaziale di un buco nero estremo dilatonico.

 

Tuttavia le geodetiche ``time-like'' relative a questa distanza, e parametrizzate rispetto al tempo proprio ( $\tau = \tau (\rho)$), si mantengono finite eccetto che nel limite GHS:

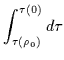$$\int_{\tau(\rho_0)}^{\tau(0)} d\tau \int_{\rho_0}^{0} d\rho\left[-\left(1+\frac{\alpha}{\rho}\right)^{-2}+ E_{\tau}^2 \left(1+\frac{\alpha}{\rho}\right)^{k-1}\right]^{-1/2}$$ =

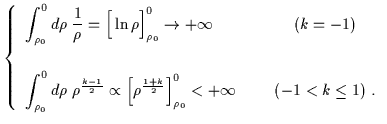$$\stackrel{\rho \to 0}{\simeq} \left\{\begin{array}{lc}\displaystyle\int_{\rho_0}^{0} d\rho \......nfty& \;\;\;\;\; (-1 < k \le 1) \; .\nonumber\\\end{array}\right.\nonumber$$ (6.28)

 

Infine le geodetiche ``light-like'', parametrizzate rispetto ad un parametro $\lambda (\rho)$ sono date da:

$$\int_{\lambda(\rho_0)}^{\lambda(0)} d\lambda \int_{\rho_0}^{0} d\rho\left(1+\frac{\alpha}{\rho}\right)^{\frac{1-k}{2}}$$ =

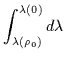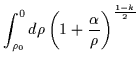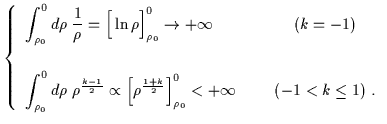$$\stackrel{\rho \to 0}{\simeq} \left\{\begin{array}{lc}\displaystyle\int_{\rho_0}^{0} d\rho \......nfty& \;\;\;\;\; (-1 < k \le 1) \; .\nonumber\\\end{array}\right.\nonumber$$ (6.29)

 

Perciò la metrica (6.21) non è geodeticamente completa, in quanto le geodetiche tipo-tempo e tipo-luce hanno un'estensione finita in tutto l'intervallo di k, eccetto che nel limite per k = -1.

Questo significa che, nel caso limite in cui il campo di modulo è disaccoppiato (k = -1), l'orizzonte $\rho = 0$ non è solo a distanza spaziale infinita, ma anche a distanza propria infinita da ogni osservatore causale; invece, in tutti gli altri casi, compreso quello della relatività generale ( $-1 < k \le 1$), una particella impiega un tempo proprio finito per raggiungere l'orizzonte, oltre il quale però, in generale, la soluzione non può essere definita. La superficie $\rho = 0$ è dunque singolare se $k \ne \pm 1$, sia pure in modo più lieve che nel caso di una singolarità di curvatura.

È anche interessante studiare il comportamento della metrica in prossimità delle regioni asintotiche.

Vicino all'orizzonte $\rho = 0$ si ha:

$$\lim_{\rho \to 0} ds^2 -\left(\frac{\alpha}{\rho}\right)^{-(1+k)} \!dt^2 +\left(\frac{\......2 + \rho^2\left( d\vartheta^2 + \sin^2 \vartheta \, d\varphi^2 \right) \right]$$ =

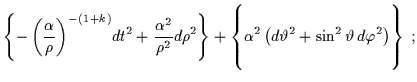$$\left\{-\left(\frac{\alpha}{\rho}\right)^{-(1+k)} \!dt^2 +\frac{......ha^2 \left( d\vartheta^2 +\sin^2 \vartheta \, d\varphi^2 \right) \right\} \; ;$$ = (6.30)

 

la metrica rappresenta, come nel caso particolare di Reissner-Nordström estremo, uno spazio di Bertotti-Robinson, costituito dalla somma di due termini. La quantità al primo termine rappresenta uno spazio-tempo bidimensionale di curvatura costante:

$$R = - \frac{1}{2} \alpha^{-2} (1 + k)^2 \; ,$$ (6.31)

 

e rappresenta quindi una pseudosfera H² (spazio anti-de Sitter) di curvatura costante negativa per tutti i valori di k compresi nell'intervallo $-1 < k \le 1$, e si riduce allo spazio piatto per il solo caso GHS (k = -1). La quantità al secondo termine è la sfera S² di raggio $\alpha$, cioè uno spazio bidimensionale di curvatura costante positiva.

Inoltre nel limite estremo, vicino all'orizzonte, il campo magnetico assume il valore costante:

$$F_{ij} = \frac{\sqrt{1-k}}{2\alpha} \,\varepsilon_{ij} \; .$$ (6.32)

 

Infine, per $\rho \to \infty$ si ha:

$$\lim_{\rho \to 0} ds^2 =- dt^2 + d\rho^2 +\rho^2 \left( d\vartheta^2 + \sin^2 \vartheta \, d\varphi^2 \right)\; ,$$ (6.33)

 

per cui la metrica è asintoticamente piatta all'infinito per ogni k, con il campo magnetico che tende a zero come un monopolo.

 
1999-03-18