| |
(4.3) |
Più precisamente, essa fornisce un insieme di equazioni di campo di estrema eleganza e compattezza, che correlano la curvatura dello spazio e del tempo con la distribuzione di materia e di energia nello spazio.
In forma covariante esse sono date da:
| |
(4.3) |
dove ![]() è il tensore energia-impulso. Tale tensore dipende dalla distribuzione
di materia e di energia di campo (esclusa quella gravitazionale). Esso
influenza le proprietà geometriche dello spazio - legate agli aspetti
gravitazionali - che sono descritte dal tensore di Ricci:
è il tensore energia-impulso. Tale tensore dipende dalla distribuzione
di materia e di energia di campo (esclusa quella gravitazionale). Esso
influenza le proprietà geometriche dello spazio - legate agli aspetti
gravitazionali - che sono descritte dal tensore di Ricci:
| (4.4) |
dove ![]() è il tensore metrico,
è il tensore metrico, ![]() è il tensore di curvatura di Riemann contratto
è il tensore di curvatura di Riemann contratto ![]() ,
e
,
e ![]() è
il tensore di curvatura di Riemann:
è
il tensore di curvatura di Riemann:
| (4.5) |
Il tensore di Riemann dipende solo dalle componenti del tensore metrico e dalle sue derivate prime e seconde, attraverso i simboli di Christoffel del I tipo definiti da:
| (4.6) |
La traccia del tensore contratto ![]() :
:
è lo scalare di curvatura.
La proporzionalità tra tensore energia-impulso e tensore di Ricci è espressa, in unità di Lorentz-Heaviside (sistema di Gauss razionalizzato), dalla costante:
dove G è la costante di gravitazione universale.
Le equazioni di campo gravitazionali possono essere facilmente espresse in una forma variazionale. Infatti, consideriamo l'azione:
| I | = | 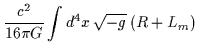 |
|
| = | 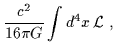 |
(4.7) |
dove:
è la densità di Lagrangiana. È noto che:
| (4.8) |
Inoltre, se:
è una densità scalare che dipende dalle componenti del
tensore metrico ![]() e da eventuali altre variabili di campo (potenziali elettromagnetici, campi
di velocità etc.), tale che:
e da eventuali altre variabili di campo (potenziali elettromagnetici, campi
di velocità etc.), tale che:
| (4.9) |
allora, la condizione che l'azione sia stazionaria per variazioni della
metrica che si annullano su ![]() (il contorno della regione compatta M), equivale a risolvere le equazioni
di Euler-Lagrange, relative ai campi
(il contorno della regione compatta M), equivale a risolvere le equazioni
di Euler-Lagrange, relative ai campi ![]() :
:
| (4.10) |
queste portano direttamente alle equazioni di Einstein (4.3).
La variazione dell'azione I rispetto al tensore metrico non descrive
però completamente il sistema fisico, ma solo i suoi aspetti gravitazionali.
È però possibile scegliere l'espressione Lm
in modo tale che la variazione di I rispetto alle variabili di campo
addizionali associate a ![]() ,
dia luogo alle equazioni di campo relative a queste variabili. In questo
caso il principio variazionale esteso
,
dia luogo alle equazioni di campo relative a queste variabili. In questo
caso il principio variazionale esteso ![]() ,
dà una descrizione completa del sistema fisico.
,
dà una descrizione completa del sistema fisico.
Tuttavia, limitandosi alla sola variazione della metrica, l'azione non
sarà un estremo se si hanno variazioni di ![]() che si annullano sul contorno, ma le cui derivate normali
che si annullano sul contorno, ma le cui derivate normali ![]() non si annullano sullo stesso [21]. La ragione
di ciò è che lo scalare di curvatura R contiene termini
lineari nelle derivate seconde della metrica e perciò, integrando
per parti, la variazione in questi termini può essere convertita
in un integrale sul bordo
non si annullano sullo stesso [21]. La ragione
di ciò è che lo scalare di curvatura R contiene termini
lineari nelle derivate seconde della metrica e perciò, integrando
per parti, la variazione in questi termini può essere convertita
in un integrale sul bordo ![]() che contiene le derivate normali della metrica nel contorno.
che contiene le derivate normali della metrica nel contorno.
Per eliminare questo integrale di superficie e ottenere un'azione che sia stazionaria per soluzioni delle equazioni di Einstein rispetto alle variazioni della metrica, bisogna aggiungere all'azione un termine della forma:
| (4.11) |
dove K è la traccia della seconda forma fondamentale ( o curvatura estrinseca [6]) del contorno, 3g è la metrica in tre dimensioni indotta sul contorno, il cui segno è positivo o negativo a seconda che il contorno sia tipo-spazio o tipo-tempo.
La necessità di aggiungere il termine di superficie alla azione nell'approccio dell'integrale di Feynman, si può vedere considerando la situazione mostrata in figura, dove si considera la transizione da una metrica 3gi sulla superficie 3Mi alla metrica 3gint sulla superficie 3Mint, e infine alla metrica 3gf sulla superficie 3Mf.
Si vuole che l'ampiezza dallo stato iniziale a quello finale sia ottenuta sommando su tutti gli stati sulla superficie intermedia 3Mint, cioè:
| (4.12) |
Questo sarà vero se e solo se:
| |
(4.13) |
dove g1 è la metrica tra 3Mi e 3Mint, e g2 è la metrica tra 3Mint e 3Mf e infine [g1 + g2] è la metrica sulla regione tra 3Mi e 3Mf.
Poiché la derivata normale di g1 in 3Mint
è in generale diversa da quella di g2 in 3Mint,
la metrica [g1 + g2]
avrà una funzione ![]() di Dirac nel tensore di Ricci, di valore 2(K1
- K2), dove K1 e K2
sono le seconde forme fondamentali sulla superficie 3Mint
nelle metriche g1 e g2 rispettivamente,
definite rispetto alla normale diretta nel futuro. Questo significa che
la relazione (4.13) sarà vera se
e solo se l'azione è data da:
di Dirac nel tensore di Ricci, di valore 2(K1
- K2), dove K1 e K2
sono le seconde forme fondamentali sulla superficie 3Mint
nelle metriche g1 e g2 rispettivamente,
definite rispetto alla normale diretta nel futuro. Questo significa che
la relazione (4.13) sarà vera se
e solo se l'azione è data da:
| (4.14) |