5.1  L'elemento di linea di Schwarzschild

Le equazioni di campo di Einstein per lo spazio privo di materia si possono ottenere a partire dall'azione:

$$I = \int d^4x \, \sqrt{-g} \, R \;,$$ (5.1)

 

e variando rispetto alle componenti del tensore metrico; le equazioni risultanti:

$$R_{\mu \nu} = 0$$ (5.2)

 

sono però non lineari, e perciò difficili da risolvere.

Tuttavia, imponendo delle condizioni di simmetria - dettate da requisiti fisici - sull'elemento di linea, si possono semplificare notevolmente le equazioni di campo in casi particolari.

Un tale caso è l'elemento di linea indipendente dal tempo e sfericamente simmetrico; le equazioni di campo risultanti sono state risolte esattamente da Schwarzschild nel 1916.

Questa soluzione è di particolare importanza poiché corrisponde al problema fondamentale ad un corpo della astronomia classica. In effetti le sole verifiche sperimentali attendibili delle equazioni di campo (5.2), come la precessione del perielio dell'orbita di Mercurio, il red-shift gravitazionale e l'incurvamento dei raggi luminosi in presenza di un campo gravitazionale, sono basati sull'elemento di linea di Schwarzschild [1].

La richiesta che una soluzione per le equazioni di campo (5.2), espressa in coordinate polari sferiche, sia indipendente dal tempo e radialmente simmetrica, è esprimibile dall'elemento di linea:

$$ds^2 = -e^{\nu (r)}c^2 dt^2 + e^{\lambda (r)}dr^2+r^2 (d\vartheta^2 + \sin^2\vartheta \, d\varphi^2 ) \; .$$ (5.3)

 

La condizione aggiuntiva che tale soluzione tenda asintoticamente alla metrica di Minkowski (spazio piatto) a grandi distanze (condizione di regolarità asintotica), è esprimibile dalle condizioni al contorno:

$$\lim_{r \to \infty} \nu (r) = \lim_{r \to \infty} \lambda (r) = 0 \; .$$ (5.4)

 

Dal tensore metrico corrispondente:

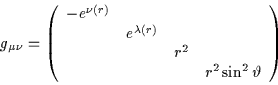$$g_{\mu \nu} = \left(\begin{array}{cccc}-e^{\nu (r)}& & & \......& & r^2 & \\& & &r^2 \sin^2 \vartheta\end{array}\right)$$ (5.5)

 
si ricavano facilmente le componenti $R_{\mu \nu}$, per cui, applicando le (5.2), si ricava che l'elemento di linea deve avere la forma:

$$ds^2 = - \left( 1- \frac{r_s}{r} \right) c^2 dt^2 +\left( 1......2 +r^2( d\vartheta^2 + \sin^2 \vartheta \, d\varphi^2 ) \; ,$$ (5.6)

 

dove:

$$r_s =\frac{2GM}{c^2}$$ (5.7)

 

è il raggio di Schwarzschild, essendo M la massa del corpo che genera il campo.

L'importanza di questo elemento di linea è che esso non rappresenta solo il campo gravitazionale di una stella (sfericamente simmetrica), ma anche un buco nero sferico neutro.

Si noti che per r = r_s accade qualcosa di anomalo; infatti l'elemento

$$g_{00} = - \left( 1- \frac{r_s}{r} \right)$$

tende a zero, mentre l'elemento

$$g_{11} = \left( 1- \frac{r_s}{r} \right)^{-1}$$

diverge. Da quanto detto finora non è chiaro se la singolarità sia insita nella geometria o se sia invece dovuta ad una scelta sbagliata delle coordinate (come per esempio si verifica nel caso dei due poli di una sfera S² parametrizzata in coordinate polari sferiche). In casi come questo si controlla se le singolarità possano essere rimosse introducendo un nuovo sistema di coordinate; il criterio più semplice è basato sull'esame della regolarità dei tre invarianti [2]:

$$R = R_{\mu}^{\mu} ;\;\;\;R_{\mu \nu}R^{\mu \nu} ;\;\;\;R_{\mu \nu \rho \sigma}R^{\mu \nu \rho \sigma}$$ (5.8)

 

associati al tensore di curvatura; questi sono tutti regolari nella superficie presunta singolare r =r_s.

Questo fatto suggerisce che nessuna vera singolarità sia presente, ma piuttosto che sia il solo sistema di coordinate che diventa singolare.

Per meglio comprendere le condizioni fisiche nell'intorno della superficie r=r_s, consideriamo le geodetiche più semplici, le radiali, quelle per cui $\vartheta, \varphi = cost.$ :

$$ds^2 = - \left( 1- \frac{r_s}{r} \right) c^2 dt^2 +\left( 1- \frac{r_s}{r} \right)^{-1}dr^2 .$$ (5.9)

 

Nel caso di un fotone è ds²=0, (geodetica ``light-like''); in tal caso la coordinata tempo t=t(r), cioè il tempo misurato da un osservatore a riposo posto all'infinito, è:

$$dt = -\frac{1}{c} \left( 1 - \frac{r_s}{r} \right)^{-1} dr \; ,$$ (5.10)

 

e quindi il fotone, per attraversare la distanza finita:

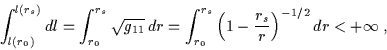$$\int_{l(r_0)}^{l(r_s)} dl = \int_{r_0}^{r_s} \sqrt{g_{11}} \,......s} \left( 1 - \frac{r_s}{r} \right)^{-1/2} dr< + \infty \; ,$$ (5.11)

 

impiega, per un osservatore distante, un tempo infinitamente lungo:

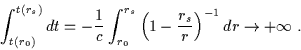$$\int_{t(r_0)}^{t(r_s)} dt = -\frac{1}{c} \int_{r_0}^{r_s}\left( 1 - \frac{r_s}{r} \right)^{-1} dr\to + \infty \; .$$ (5.12)

 

Analoga considerazione vale per una particella materiale (ds² < 0: geodetica ``time-like''); in tal caso la funzione t=t(r) è:

$$dt = - \frac{E_{\tau}}{c} \left( 1- \frac{r_s}{r} \right)^{-1......t( -c^2 + E_{\tau}^2 +c^2 \frac{r_s}{r} \right)^{-1/2} dr \; ,$$ (5.13)

 

dove:

$$E_{\tau}^2 = \left( 1- \frac{r_s}{r} \right)^2 c^2\left( \frac{dt}{d\tau} \right)^2 \; ,$$ (5.14)

 

e quindi, integrando nello stesso intervallo:

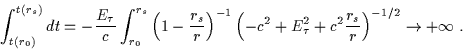$$\int_{t(r_0)}^{t(r_s)} dt = - \frac{E_{\tau}}{c} \int_{r_0}^{......_{\tau}^2 +c^2 \frac{r_s}{r} \right)^{-1/2}\to + \infty \; .$$ (5.15)

 

Tuttavia la particella materiale misura un tempo proprio $\tau$(definito da $ds^2 = -c^2 d\tau^2$ ) che, esplicitando rispetto alla coordinata radiale è :

$$d\tau = - \left( -c^2 +E_{\tau}^2 + c^2\frac{r_s}{r} \right)^{-1/2} dr \; ;$$ (5.16)

 

integrando nello stesso intervallo:

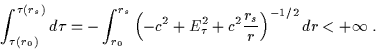$$\int_{\tau(r_0)}^{\tau(r_s)} d\tau = - \int_{r_0}^{r_s}\le......{\tau}^2 + c^2\frac{r_s}{r} \right)^{-1/2} dr< + \infty \; .$$ (5.17)

 

Questo è un caso estremo di dilatazione dei tempi, in cui un intervallo di tempo finito è visto come infinito da un osservatore distante.

Perciò, nel momento in cui una particella attraversa la superficie r = r_s, non accade nulla di particolare, non essendo presente alcuna singolarità metrica. Ma se la particella emette radiazione, un osservatore distante vedrà la sua luce spostata verso il rosso, poiché la sorgente è sotto l'influenza di un forte campo gravitazionale. Nel momento in cui essa raggiunge l'orizzonte, il red-shift è così forte che la radiazione non è più visibile in alcuna regione dello spettro.

Similmente il tempo proprio misurato da una particella per raggiungere la singolarità r=0 partendo da r =r_s è anch'esso finito:

$$- \int_{r_s}^{0}\left( -c^2 +E_{\tau}^2 + c^2\frac{r_s}{r} \right)^{-1/2} dr< + \infty \; .$$ (5.18)

 

Perciò una particella all'interno di r=r_s inevitabilmente raggiungerà la singolarità centrale, in cui la densità e la curvatura dello spazio-tempo diventano infinite e le leggi della relatività generale non sono più applicabili.

Inoltre, eventuali segnali mandati dall'interno della superficie r=r_s devono viaggiare verso il futuro temporale ma, all'interno di tale regione, il tempo crescente equivale a distanze radiali decrescenti. Ciò si può vedere considerando, per r>r_s l'intervallo tipo-tempo:

$$ds^2 = - \left( 1 - \frac{r_s}{r} \right)\, c^2 \, dt^2 < 0 \; ;$$ (5.19)

 

questo, per r<r_s, diventa positivo e quindi tipo-spazio, per cui, all'interno di r=r_s le coordinate radiale e temporale si scambiano di ruolo [5].

Dunque, il fotone e qualunque altra particella materiale, una volta arrivati alla superficie r=r_s, non hanno alcuna possibilità di emergere; questa superficie è perciò chiamata un orizzonte degli eventi. Così, dal punto di vista di un osservatore distante, il collasso gravitazionale genera la comparsa di un corpo ``congelato'' che non può emettere alcun segnale. Un tale sistema materiale viene chiamato buco nero.

 
1999-03-18