5.2  La soluzione di Reissner-Nordström

Anche in considerazione degli sviluppi seguenti è opportuno ricordare i buchi neri carichi di Reissner-Nordström. La corrispondente soluzione esprime il campo esterno statico e sfericamente simmetrico di una distribuzione di massa carica [24].

Le equazioni di campo si possono ottenere, tramite un approccio variazionale, a partire dall'azione di Einstein-Maxwell che, in unità per cui $c = G = \hbar = C = 1$, è:

$$I = \int d^4x \, \sqrt{-g} \, \left[ R - \frac{1}{2} \, F^2 \right] \; .$$ (5.20)

 

La variazione rispetto alle componenti del tensore metrico $g^{\mu \nu}$porta allora alle equazioni di campo generali di Einstein (4.3):

$$G_{\mu \nu}= T_{\mu \nu} \; ,$$

dove:

$$T_{\mu \nu} = \left[ F_{\mu \alpha} F_{\nu}^{\;\:\alpha} -\frac{1}{4} F_{\rho \tau} F^{\rho \tau} g_{\mu \nu} \right]$$ (5.21)

 

è il tensore energia-impulso dovuto al campo elettromagnetico .

Una coppia delle equazioni di Maxwell si può esprimere nella forma covariante:
 
 

$$\left\{\partial_{\lambda} F_{\mu \nu} \right\} = 0 \; ,$$ (5.22)

 

dove $\{_{\lambda \; \mu \; \nu}\}$è l'operatore di antisimmetrizzazione su tutte le permutazioni di $(\lambda, \mu, \nu)$. Come è noto, questa relazione esprime il fatto che il tensore di campo elettromagnetico $F_{\mu \nu}$è un tensore antisimmetrico chiuso e, come tale, è anche esatto [1], cioè ammette un potenziale vettore; perciò $F_{\mu \nu}$può essere scritto nella forma:

$$F_{\mu \nu} = \partial_{\mu}A_{\nu} - \partial_{\nu}A_{\mu} \; ;$$ (5.23)

 

in tal modo le (5.22) sono automaticamente soddisfatte.

A questo punto, variando l'azione rispetto al potenziale vettore $A_{\mu}$, si può ottenere in forma covariante la seconda coppia delle equazioni di Maxwell per regioni dello spazio prive di cariche:

$$\frac{1}{\sqrt{-g}} \, \partial_{\mu}\left(\sqrt{-g} \, F^{\mu \nu} \right) = 0 \; ,$$ (5.24)

 

o, in forma più compatta:

$$\nabla_{\mu} F^{\mu \nu} = 0 \; ,$$ (5.25)

 

dove $\nabla_{\mu}$ è l'operatore di differenziazione covariante definito da:

$$\nabla_{\mu} \xi^{\nu} =\partial_{\mu} \xi^{\nu} + \Gamma^{\nu}_{\mu \rho} \xi^{\rho} \; .$$ (5.26)

 

La risoluzione delle equazioni di campo porta allora all'elemento di linea di Reissner-Nordström che, nelle unità usate, si può scrivere nella forma:

 

$$- \left( 1- \frac{2M}{r} +\frac{Q^2}{r^2} \right) dt^2 +\left( 1- \frac{2M}{r} +\frac{Q^2}{r^2} \right)^{-1}dr^2$$                         ds² =

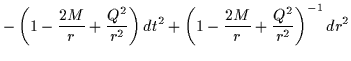$$+ r^2\left( d\vartheta^2 + \sin^2 \vartheta\, d\varphi^2 \right) \; ,$$ (5.27)

 

dove M è un parametro associato alla massa che crea il campo e Q è un parametro correlato alla carica elettrica o magnetica.

In particolare, nel caso di carica magnetica, che ci interesserà in seguito ^5.1, la soluzione per le componenti angolari del tensore $F_{\mu \nu}$ è data da:

$$F_{ij} = \frac{Q}{r^2} \varepsilon_{ij}\;\;\;\;\;\;\;\;\; \left( i,j = (2,3) \, \right) \; .$$ (5.28)

 

Poiché, per grande r, il termine $\frac{Q^2}{r^2}$nella metrica può essere ignorato e dato che i corpi celesti in pratica non sono carichi, l'influenza del campo elettromagnetico sulla metrica è trascurabile in astrofisica. Tuttavia l'influenza del termine $\frac{Q^2}{r^2}$ può diventare importante a livello microscopico, quando gli effetti della meccanica quantistica dominano.

Si noti che la soluzione di Reissner-Nordström (5.27) mostra divergenze nelle componenti della metrica in r = 0 e negli zeri di g₀₀, ossia:

$$r_{\pm} = M \pm \sqrt{M^2 - Q^2} \; .$$ (5.29)

 

Come per la soluzione di Scwarzschild, la singolarità in r=0è una singolarità di curvatura non rimovibile (anche se di diversa natura [25]), mentre quelle in $r = r_{\pm}$sono singolarità di coordinate che possono essere eliminate con una opportuna estensione analitica della metrica. In questo caso tuttavia bisogna distinguere i tre casi: M² > Q², M² = Q² e M² < Q².

1. Per M² > Q², le due radici $r = r_{\pm}$ sono reali e distinte. Uno studio delle geodetiche radiali dimostra che la superficie esterna r = r₊ rappresenta un orizzonte degli eventi posto a distanza spaziale finita da un qualunque punto esterno ad essa. La superficie interna r = r_- rappresenta un altro tipo di orizzonte, detto di Cauchy, che sembra essere instabile per piccole perturbazioni [37].

2. Per M² = Q², si ha il caso definito massimamente carico, o estremo, in cui la metrica è singolare in r = 0 e i due orizzonti si fondono nell'unico orizzonte r = r₊ = r_- = M.

3. Per M² < Q², la metrica presenta una sola singolarità in r = 0, in quanto le due radici $r = r_{\pm}$ nella (5.29) diventano complesse. Tuttavia in questo caso una sfera materiale non può subire il collasso gravitazionale perché, per M² < Q²la repulsione coulombiana prevarrebbe sull'attrazione gravitazionale. L'assenza di orizzonti e l'impossibilità del collasso suggeriscono ciò che Penrose, nel 1969, ha definito come ``ipotesi della censura cosmica'', la quale sostiene che, dal collasso gravitazionale di un oggetto materiale, non si possano formare delle singolarità - in cui le leggi della fisica cessano di valere -, a meno che queste non siano nascoste da un orizzonte; cioè singolarità nude non possono nascere spontaneamente a partire da una situazione iniziale regolare (naturalmente tale ipotesi non preclude la possibilità di singolarità già esistenti, come quella del big-bang).

Per quanto detto la condizione M² = Q² rappresenta il caso limite di un buco nero estremo massimamente carico, in cui la repusione coulombiana è tale da bilanciare esattamente l'attrazione node0.oniana [25].

L'importanza del buco nero estremo carico è data anche dal fatto che, secondo i risultati di Hawking [27], un buco nero carico di massa M > Q tende, a causa di un processo quantistico (come vedremo nel prossimo paragrafo), ad evaporare, sino a raggiungere il valore estremo M = Q, al qual punto la temperatura di Hawking si annulla e l'evaporazione cessa. Perciò si ritiene che le soluzioni estreme siano il punto terminale del processo di evaporazione di Hawking e corrispondano a stati fondamentali stabili [26,43].

Nel caso estremo la metrica di Reissner-Nordström assume la forma:

$$ds^2 = - \left( 1- \frac{M}{r} \right)^2 \! dt^2 +\left( 1-......\vartheta^2 \! + \sin^2 \vartheta\, d\varphi^2 \right) \: .$$ (5.30)

 

Con il cambiamento di coordinate $r = \rho + m$, si ha:

$$1 - \frac{M}{r} = \left( 1 + \frac{M}{\rho} \right)^{-1} \; ,$$ (5.31)

 

e quindi l'elemento di linea si può scrivere in coordinate isotrope nella forma conforme :

$$ds^2 = - \left( 1 + \frac{M}{\rho} \right)^{-2} dt^2 +\left...... (d\vartheta^2 + \sin^2 \vartheta \, d\varphi^2 ) \right] \; .$$ (5.32)

 

Si noti che, con questa trasformazione, si è ottenuto un elemento di linea che è indipendente dalle particolari coordinate spaziali usate e che più si avvicina alla nozione intuitiva di spazio basata sulla geometria euclidea.
 

 
1999-03-18