5.2.1  Proprietà della metrica estrema

Lo studio delle geodetiche radiali della metrica estrema di Reissner-Nordström ci fornisce utili informazioni sulla struttura della geometria spazio-temporale [5]; si ha infatti che l'orizzonte $\rho = 0$ si trova, a differenza dell'orizzonte di Schwarzschild, a distanza spaziale infinita da un qualunque punto esterno $\rho_0\:$:

$$\int_{l(\rho_0)}^{l(0)} dl = \int_{\rho_0}^0\left( 1 + \fra......m}{.4cm} \rho + M \ln \rho \right]_{\rho_0}^0\to \infty \; .$$ (5.33)

 

Tuttavia la distanza propria misurata da una particella per raggiungere l'orizzonte da un punto esterno, si mantiene finita:

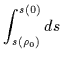$$\int_{s(\rho_0)}^{s(0)} ds \int_{\rho_0}^0\left[\left( 1 + \frac{M}{\rho} \right)^{-2} + E^2\right]^{-1/2} d\rho$$ =

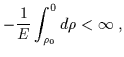$$\stackrel{\rho \to 0}{\simeq} - \frac{1}{E} \int_{\rho_0}^0 d\rho< \infty \; ,$$ (5.34)

 

dove il parametro E è definito da:

$$E = \left( 1 + \frac{M}{\rho} \right) \frac{dt}{ds} \; .$$ (5.35)

 

Inoltre, come nel caso di Schwarzschild e in quello di Reissner-Nordström non estremo, la metrica è asintoticamente piatta all'infinito:

$$\lim_{\rho \to \infty} ds^2 =- dt^2 + d\rho^2 + \rho^2 \left( d\vartheta^2 + \sin^2 \vartheta \,d\varphi^2 \right) \; ,$$ (5.36)

 

mentre in prossimità dell'orizzonte $\rho = 0$ è:

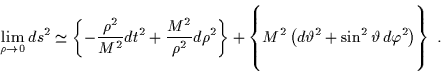$$\lim_{\rho \to 0} ds^2 \simeq\left\{-\frac{\rho^2}{M^2} dt^......heta^2 +\sin^2 \vartheta \, d\varphi^2 \right) \right\} \; .$$ (5.37)

 

La metrica è data dalla somma di due termini indipendenti. La quantità al primo termine rappresenta uno spazio-tempo bidimensionale di curvatura costante negativa:

$$R = - \frac{2}{M^2}$$ (5.38)

 

e definisce la metrica di una pseudosfera H²; la quantità al secondo membro rappresenta invece una sfera S², cioè uno spazio bidimensionale di curvatura costante positiva. Pertanto, in prossimità dell'orizzonte, la soluzione ha la forma:

$$H^2 \times S^2 \; ,$$ (5.39)

 

e tale spazio viene detto di Bertotti-Robinson [28,29].

 
1999-03-18