3.1  Istantoni in meccanica quantistica

La maggior parte delle soluzioni istantoniche sono non perturbative, cioè non possono essere ottenute a partire dalle soluzioni della corrispondente parte lineare delle equazioni di campo, e quindi trattando i termini non lineari in modo perturbativo.

Per illustrare la fisica degli istantoni, consideriamo un semplice esempio in meccanica quantistica: il moto di una particella di massa m che si muove in un potenziale unidimensionale, del tipo mostrato in figura.

 

Figura 3.1: Il potenziale V(q).

 

Classicamente questo moto è descritto dalla Lagrangiana:

$$L=\frac{1}{2}m\dot{q}^2-V(q) \; .$$ (3.7)

 

Dal punto di vista quantistico, a questo sistema è associata l'Hamiltoniana:

$$H(P,Q)=\frac{P^2}{2m}+V(Q) \; .$$ (3.8)

 

Se consideriamo il fenomeno del tunnelling attraverso una barriera di potenziale definita dalla funzione V(q), l'ampiezza di transizione è un risultato noto in meccanica quantistica, dato dalla approssimazione di Wentzel, Kramers, Brillouin (WKB):

$$T(E)=e^{-\frac{1}{\hbar}\int_{q_i}^{q_f}dq\sqrt{2m[V(q)-E]}} \; [1+O(\hbar)] \; ,$$ (3.9)

 

dove T(E) rappresenta l'ampiezza di transizione della barriera e dove q_i e q_f sono i punti di inversione classici all'energia E.

Come è noto, questa espressione è ottenuta a partire da una approssimazione semiclassica, cioè una approssimazione di piccolo $\hbar$.

Questa approssimazione è applicabile quando la lunghezza d'onda di de Broglie $\lambda =h/p$ associata alla particella è piccola rispetto alle dimensioni caratteristiche del sistema in esame; in questo caso le proprietà del sistema sono vicine a quelle classiche [4].

Questo tipo di approssimazione viene effettuato considerando, nella equazione di Schrödinger indipendente dal tempo:

$$\frac{\hbar ^2}{2m} \mbox{\boldmath$\nabla$ } ^2 \psi +[E-V(q)] \; \psi =0$$ (3.10)

 

la sostituzione formale:

$$\psi = e^{\frac{i}{\hbar}S(q)} \; ;$$ (3.11)

 

si cerca, per la funzione S(q), uno sviluppo in serie di potenze di $\hbar$:

$$S=S_0+\frac{\hbar}{i}S_1+\left(\frac{\hbar}{i}\right)^2 S_2 + \cdots \; .$$ (3.12)

 

Allora, poiché il sistema è supposto semiclassico nelle sue proprietà, solamente i primi termini di questo sviluppo danno un contributo alla funzione d'onda.

Applicando questo tipo di procedimento al calcolo della probabilità di tunnelling attraverso una barriera di potenziale, si arriva alla già citata approssimazione WKB (3.9), valida per potenziali lentamente variabili e lontano dai punti di inversione.

Ciononostante il fenomeno del tunnelling non può essere visto in alcun ordine di una teoria delle perturbazioni, in quanto l'ampiezza T(E) si annulla più rapidamente di ogni potenza di $\hbar$.

Poiché, per il problema in esame, conosciamo l'ampiezza di tunnelling calcolata con un metodo noto (approssimazione WKB), cercheremo di riderivare alcune proprietà formali di questo sistema tramite i metodi basati sulla fisica degli istantoni. Lo strumento essenziale sarà la versione euclidea dell'integrale di cammino di Feynman [16,17].

La propagazione di una particella in meccanica quantistica, nella formulazione dell'integrale di cammino espresso nello spazio delle configurazioni, è descritta, come già ricavato nel precedente capitolo, dal kernel:

$$\langle q_{f}\vert e^{-\frac{i}{\hbar}H(t_f-t_i)}\vert q_i\rangle$$ K(q_f,q_i;t_f-t_i) =

$$\int {\cal D} [q(t)] \; e^{\frac{i}{\hbar}I[q(t)]} \; ,$$ = (3.13)

 

dove l'azione minkowskiana è:

$$I = \int_{t_i}^{t_f}dt \left[\frac{1}{2}m\dot{q}^2-V(q)\right] \; .$$ (3.14)

 

Come sappiamo, K è l'ampiezza di transizione per cui una particella nel potenziale V(q) osservata in q_i all'istante t_i, sarà osservata in q_f all'istante t_f.

La versione euclidea di questa espressione si ottiene tramite la rotazione di Wick dell'asse dei tempi:

$$t \to it = \tau \;\;\;\;\; \Leftrightarrow \;\;\;\;\; t=-i \tau \; .$$ (3.15)

 

In questo caso l'azione diventa:

$$\int_{\tau_i}^{\tau_f}-i \, d\tau \left[-\frac{1}{2}m\left(\frac{dq}{-i \, d\tau}\right)^2+V(q)\right]$$                        I =

$$i \int_{\tau_i}^{\tau_f}d\tau \left[\frac{1}{2}m\left(\frac{dq}{d\tau}\right)^2+V(q)\right]$$ =

$$i \, I_E \; ,$$ = (3.16)

 

dove:

$$I_E=\int_{\tau_i}^{\tau_f}d\tau \left[\frac{1}{2}m\left(\frac{dq}{d\tau}\right)^2+V(q)\right]$$ (3.17)

 

è l'azione euclidea; perciò:

$$e^{\frac{i}{\hbar}I[q(t)]}\to e^{\frac{i}{\hbar}iI_E[q(\tau)]}= e^{-I_E[q(\tau)/\hbar]} \; .$$ (3.18)

 

Inoltre:

$$H(t_f-t_i)\to H[-i(\tau_f -\tau_i)]= -iH(\tau_f -\tau_i) \; ,$$ (3.19)

 

da cui:

$$e^{-\frac{i}{\hbar}H(t_f-t_i)}\to e^{-\frac{i}{\hbar}(-i)H(\tau_f -\tau_i)}= e^{-H(\tau_f -\tau_i)/\hbar} \; ,$$ (3.20)

 

e quindi l'ampiezza di transizione diventa:

 

$$K_E(q_f,q_i;\tau_f-\tau_i) \langle q_{f}\vert e^{-H(\tau_f-\tau_i)/\hbar}\vert q_i\rangle$$ =

$$\int {\cal D} [q(\tau)] \; e^{-I_E[q(\tau)]/\hbar} \; .$$ = (3.21)

 

L'espressione $\langle q_{f}\vert e^{-H(\tau_f-\tau_i)/\hbar}\vert q_i\rangle$ è interessante perché, se consideriamo un insieme completo di autostati di energia:

$$H\vert n\rangle =E_n\vert n\rangle \; ,$$ (3.22)

 

allora:

$$\langle q_{f}\vert e^{-H(\tau_f-\tau_i)/\hbar}\vert q_i\rangle \sum_n \langle q_{f}\vert e^{-H(\tau_f-\tau_i)/\hbar}\vert n\rangle \langle n \vert q_i\rangle$$ =

$$\sum_n e^{-E_n(\tau_f-\tau_i)/\hbar}\langle q_{f}\vert n\rangle \langle n \vert q_i\rangle .$$ = (3.23)

 

Dunque, per grandi intervalli $\tau_f - \tau_i \;$, il termine dominante di questa espressione è quello corrispondente alla funzione d'onda dell'autostato di minore energia (stato fondamentale).

L'ultimo membro della (3.21), cioè l'integrale di Feynman nello spazio euclideo è altrettanto interessante, perché può essere facilmente calcolato nel limite semiclassico, tramite l'approssimazione di fase stazionaria, anche nota come metodo del punto a sella [18].

Secondo questa approssimazione, se (I_E)_cl è l'azione classica - cioè l'azione per cui è $\delta I_E = 0$ - allora, nel limite di piccolo $\hbar$ l'integrale è asintoticamente uguale a:

$$\int {\cal D} [q(\tau)] \; e^{-I_E[q(\tau)]/\hbar}\simeq C \times e^{-(I_E)_{cl}/\hbar} \; .$$ (3.24)

 

Applichiamo ora questa approssimazione al potenziale introdotto in precedenza, denotando i suoi minimi con q_i e q_f.

L'azione euclidea è data dalla (3.17):
 $$I_E=\int_{\tau_i}^{\tau_f}d\tau \left[\frac{1}{2}m\left(\frac{dq}{d\tau}\right)^2+V(q)\right] \; .$$
 

Il moto classico è descritto dalle equazioni di Euler-Lagrange:

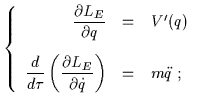$$\left\{\begin{array}{rcl}\displaystyle\frac{\partial L_E}{\par......\partial L_E}{\partial \dot{q}} \right)& = & m\ddot{q} \; ;\end{array}\right.$$ (3.25)

 

perciò:

$$-m\frac{d^2q}{d\tau^2}+V'(q) = 0 \; .$$ (3.26)

 

Questa è l'equazione del moto per una particella di massa m che si muove nel potenziale -V(q); perciò:

$$E = \frac{1}{2}m \left(\frac{dq}{d\tau}\right)^2-V(q) \; .$$ (3.27)

 
 
 

Figura 3.2: Il potenziale -V(q).

 

Due soluzioni ovvie sono quelle in cui la particella sta fissa su uno dei due massimi q_i o q_f.

Tuttavia c'è un'altra soluzione potenzialmente interessante; quella in cui la particella inizia il moto in uno dei due massimi, per esempio q_i al tempo $\tau_i$, e arriva alla cima del massimo opposto q_f al tempo $\tau_f$.

Poiché nella approssimazione che utilizziamo, dobbiamo considerare un intervallo di tempo $\tau_f - \tau_i \;$ grande, focalizzeremo l'attenzione sulla soluzione per cui la particella passa da un massimo all'altro in un intervallo di tempo infinito; cioè consideriamo una soluzione dell'equazione del moto per E=0. Perciò:

$$E = \frac{1}{2}m \left(\frac{dq}{d\tau}\right)^2-V(q) = 0 \; ,$$ (3.28)

 

cioè:

$$\frac{dq}{d\tau}=\sqrt{\frac{2}{m}V(q)} \; .$$ (3.29)

 

Equivalentemente:

$$\int_{\tau_i}^{\tau_f}d\tau =\int_{q_i}^{q_f}dq \left[\frac{2}{m}V(q)\right]^{-\frac{1}{2}} \; ,$$ (3.30)

 

ossia:

$$\tau_f - \tau_i =\int_{q_i}^{q_f}dq\left[\frac{2}{m}V(q)\right]^{-\frac{1}{2}} \; .$$ (3.31)

 

Tale soluzione è chiamata un istantone.
 
 

Figura 3.3: L'istantone.

 

A questo punto è facile derivare una semplice espressione per (I_E)_cl, cioè l'azione dell'istantone:

$$\int_{\tau_i}^{\tau_f}d\tau\left[\frac{1}{2}m\left(\frac{dq}{d\tau}\right)^2 + V(q)\right]$$                    (I_E)_cl =

$$\int_{\tau_i}^{\tau_f}d\tau \,m\left(\frac{dq}{d\tau}\right)^2$$ =

$$m \int_{q_i}^{q_f}dq \, \frac{dq}{d\tau}$$ =

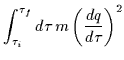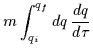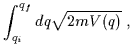$$\int_{q_i}^{q_f}dq\sqrt{2mV(q)} \; ,$$ = (3.32)

 

e, in definitiva, nell'approssimazione di fase stazionaria:

$$\langle q_{f}\vert e^{-H(\tau_f-\tau_i)/\hbar}\vert q_i\rangle \int {\cal D} [q(\tau)] \; e^{-I[q(\tau)]/\hbar}$$ =

$$\simeq e^{-(I_E)_{cl}/\hbar}$$

$$e^{-\frac{1}{\hbar} \int_{q_i}^{q_f} dq\sqrt{2mV(q)}} \; .$$ = (3.33)

 

Quest'ultima espressione costituisce il risultato fondamentale di tutta la discussione, in quanto è lo stesso integrale che appare nella formula della penetrazione in una barriera di potenziale, calcolata col metodo WKB, ottenuta però questa volta con il metodo istantonico.

 
1999-03-18