| (2.1) |
Siano q e p le coordinate di posizione e di quantità di moto di una particella, a cui corrispondono gli operatori Q e P.
Nella rappresentazione delle coordinate, gli operatori hanno la forma:
| (2.1) |
i corrispondenti autostati sono esprimibili nella forma:
| (2.2) |
questi soddisfano le equazioni agli autovalori:
| (2.3) |
Le funzioni di trasformazione dalla rappresentazione delle coordinate a quella degli impulsi e viceversa sono date da:
| |
= | 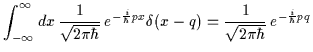 |
(2.4) |
| = | (2.5) |
La dinamica di un sistema in meccanica quantistica è descritta
dall'operatore Hamiltoniano, che qui assumiamo, per semplicità,
indipendente dal tempo, e che in generale è una funzione degli operatori
di posizione e quantità di moto:
| |
(2.6) |
Senza discutere il problema generale dell'ordinamento temporale, per definizione assumeremo che tutti gli operatori P siano posti alla sinistra di tutti gli operatori Q.
Con tale convenzione, l'elemento di matrice dell'Hamiltoniana tra gli
stati ![]() e
e ![]() ,
è espresso esplicitamente in termini della funzione classica
Hamiltoniana E(p,q):
,
è espresso esplicitamente in termini della funzione classica
Hamiltoniana E(p,q):
| |
= | ||
| = | (2.7) |
Il nostro scopo è quello di calcolare l'operatore di evoluzione temporale:
| (2.8) |
Per tale motivo calcoliamo il suo elemento di matrice, cioè l'ampiezza
di transizione dallo stato qi al tempo ti,
allo stato qf al tempo tf:
| = | |||
| = | |||
| = | (2.9) |
Tale elemento di matrice è anche chiamato il nucleo (``kernel'')
K dell'operatore U(ti,tf)
nella rappresentazione in coordinate. Per piccoli tf-ti,
è facile calcolare l'ampiezza di transizione ![]() .
Infatti in questo caso:
.
Infatti in questo caso:
| U(ti,tf) | = | ||
| = | 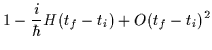 |
||
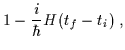 |
(2.10) |
e possiamo approssimativamente scrivere:
| = | |||
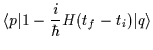 |
|||
| = | 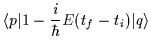 |
||
| (2.11) |
L'ultima espressione ottenuta è ingannevolmente semplice. Sebbene
l'operatore di evoluzione temporale contenga l'operatore Hamiltoniano
in forma esponenziale, il risultato finale non contiene affatto operatori.
Il punto essenziale è che per intervalli di tempo ![]() infinitesimi, abbiamo potuto mantenere nello sviluppo in serie soltanto
il termine di primo ordine; ma se, per intervalli di tempo finiti, avessimo
dovuto considerare anche i termini successivi dello sviluppo, la non commutatività
degli operatori di posizione e quantità di moto nell'Hamiltoniana,
avrebbe impedito la sostituzione di questi operatori con i corrispondenti
autovalori.
infinitesimi, abbiamo potuto mantenere nello sviluppo in serie soltanto
il termine di primo ordine; ma se, per intervalli di tempo finiti, avessimo
dovuto considerare anche i termini successivi dello sviluppo, la non commutatività
degli operatori di posizione e quantità di moto nell'Hamiltoniana,
avrebbe impedito la sostituzione di questi operatori con i corrispondenti
autovalori.
Se nell'ultima espressione inseriamo un insieme completo di operatori
di quantità di moto:
| |
(2.12) |
il kernel dell'operatore U(ti,tf) nella rappresentazione in coordinate è facilmente calcolabile:
| |
= | 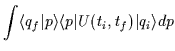 |
|
| = | 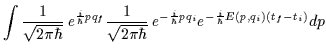 |
||
| = | ![$\displaystyle \frac{1}{2\pi\hbar} \int e^{\frac{i}{\hbar}\left[p(q_f-q_i)-E(p,q_i)(t_f-t_i)\right]}dp \; .$](img50.gif) |
(2.13) |
A questo punto si può calcolare l'ampiezza di transizione ![]() per un intervallo di tempo
per un intervallo di tempo ![]() finito. In questo caso si può procedere come segue: dividiamo l'intervallo
finito. In questo caso si può procedere come segue: dividiamo l'intervallo ![]() in N parti
in N parti ![]() ,
ognuna di grandezza:
,
ognuna di grandezza:
| |
(2.14) |
sufficientemente piccola da poter usare la formula precedente (2.9)
per l'operatore ![]() .
.
Possiamo allora esprimere l'operatore U(ti,tf) nella forma:
| (2.15) |
Perciò, inserendo degli insiemi completi di stati di posizione:
| (2.16) |
tra ognuno degli operatori di evoluzione temporale individuali, si ottiene:
| |
|||
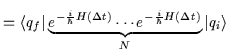 |
|||
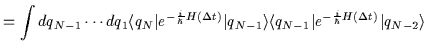 |
|||
| (2.17) | |||
dove, per chiarezza, abbiamo indicato lo stato iniziale ![]() ,
e lo stato finale
,
e lo stato finale ![]() ,
ed ogni integrale è calcolato tra
,
ed ogni integrale è calcolato tra ![]() e
e ![]() .
Riutilizzando la relazione di completezza per gli operatori
.
Riutilizzando la relazione di completezza per gli operatori ![]() - come abbiamo già fatto per il calcolo del kernel - per ognuno
degli operatori di evoluzione temporale parziale, otteniamo:
- come abbiamo già fatto per il calcolo del kernel - per ognuno
degli operatori di evoluzione temporale parziale, otteniamo:
| |
|||
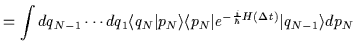 |
|||
| |
|||
| (2.18) | |||
da cui:
| |
![$\displaystyle \frac{1}{2\pi\hbar}\int e^{\frac{i}{\hbar}\left[p_N(q_N-q_{N-1})-E(p_N,q_{N-1})\Delta t \right]}dp_N$](img69.gif) |
||
![$\displaystyle \frac{1}{2\pi\hbar}\int e^{\frac{i}{\hbar}\left[p_{N-1}(q_{N-1}-q_{N-2})-E(p_{N-1},q_{N-2})\Delta t \right]}dp_{N-1}$](img71.gif) |
|||
![$\displaystyle \frac{1}{2\pi\hbar}\int e^{\frac{i}{\hbar}\left[p_1(q_1-q_0)-E(p_1,q_0)\Delta t \right]}dp_1 \; ,$](img73.gif) |
(2.19) | ||
e quindi:
![$\displaystyle = \int e^{\frac{i}{\hbar}\left[p_N(q_N-q_{N-1})+p_{N-1}(q_{N-1}-q_{N-2})+\cdots + p_1(q_1-q_0)\right]}$](img74.gif) |
|||
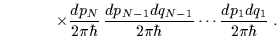 |
(2.20) | ||
Al limite per ![]() o, equivalentemente, per
o, equivalentemente, per ![]() ,
l'ultima espressione diventa:
,
l'ultima espressione diventa:
![$\displaystyle = \int e^{\frac{i}{\hbar}\int_{t_i}^{t_f}\left[p(t)\dot{q}(t)-E\left(p(t),q(t)\right)\right]dt}\prod_{t}\frac{dp \, dq}{2\pi\hbar}$](img79.gif) |
|||
![$\displaystyle = \int e^{\frac{i}{\hbar}\int_{t_i}^{t_f}L[q(t),p(t),t]dt}\prod_{t}\frac{dp \, dq}{2\pi\hbar}$](img80.gif) |
|||
![$\displaystyle = \int e^{\frac{i}{\hbar}I[q(t),p(t),t]}\prod_{t}\frac{dp \, dq}{2\pi\hbar} \; ,$](img81.gif) |
(2.21) | ||
dove:
| (2.22) |
è la Lagrangiana espressa nello spazio delle fasi, e:
| (2.23) |
è l'azione.
Abbiamo così ottenuto il risultato principale: l'elemento di
matrice dell'operatore evoluzione temporale (cioè l'ampiezza di
transizione tra i due stati considerati qi e qf),
si trova integrando il funzionale di Feynman ![]() ,
su tutte le traiettorie p(t) e q(t) nello spazio
delle fasi, con valori fissi qi e qf
agli istanti ti e tf rispettivamente.
,
su tutte le traiettorie p(t) e q(t) nello spazio
delle fasi, con valori fissi qi e qf
agli istanti ti e tf rispettivamente.
Siamo così arrivati ad una espressione quantistica funzione della sola azione classica.
Feynman stesso usò una espressione leggermente differente dell'integrale di cammino. Se infatti l'Hamiltoniana è quadratica negli impulsi:
| (2.24) |
allora l'integrazione sulle variabili p e q può essere effettuata esplicitamente. Se nell'integrale relativo a questo tipo di Hamiltoniana:
![\begin{displaymath}\int e^{\frac{i}{\hbar} \int_{t_i}^{t_f}\left[p\dot{q} - \f......}{2m} - V(q) \right]dt}\prod_{t}\frac{dp \, dq}{2 \pi \hbar}\end{displaymath}](img86.gif) |
(2.25) |
si considera la trasformazione:
| (2.26) |
allora è possibile separare l'integrazione su p e q:
![$\displaystyle = \int e^{\frac{i}{\hbar}\int_{t_i}^{t_f}\left [(p+m\dot{q})\dot......(p+m\dot{q})^2}{2m} - V(q)\right]dt}\prod_{t}\frac{d(p+m\dot{q})dq}{2\pi\hbar}$](img89.gif) |
|||
![$\displaystyle = \int e^{-\frac{i}{\hbar}\int_{t_i}^{t_f}\frac{p^2}{2m}dt}\pro......\hbar}\int_{t_i}^{t_f}\left[\frac{m \dot{q}^2}{2} - V(q)\right]dt}\prod_{t}dq$](img90.gif) |
|||
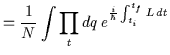 |
|||
![$\displaystyle = \int {\cal D} [q(t)] \, e^{\frac{i}{\hbar}I[q(t)]} \; ,$](img92.gif) |
(2.27) | ||
dove:
| (2.28) |
è la Lagrangiana del sistema; la quantità:
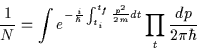 |
(2.29) |
è l'inverso del fattore di normalizzazione, che è ovviamente indipendente da qi e qf, ed è una funzione solamente dell'intervallo di tempo tf-ti; infine:
| (2.30) |
rappresenta la misura sullo spazio di tutte le configurazioni q(t).
Quest'ultima forma dell'integrale di cammino, espressa nello spazio
delle configurazioni, anche se meno generale della precedente, è
quella più conosciuta, anche perché applicabile nella maggior
parte dei casi. Espressa in questa forma, l'ampiezza di transizione ![]() si trova considerando tutte le traiettorie nel piano [q,t],
che connettono i due punti estremi. Ogni cammino q(t) dà
un contributo proporzionale a
si trova considerando tutte le traiettorie nel piano [q,t],
che connettono i due punti estremi. Ogni cammino q(t) dà
un contributo proporzionale a ![]() ,
un fattore che ha modulo unitario, e dipende dal cammino solo tramite il
fattore di fase
,
un fattore che ha modulo unitario, e dipende dal cammino solo tramite il
fattore di fase ![]() .
.
Il fatto notevole è che tutti i cammini contribuiscono all'ampiezza di transizione in ugual misura, ed è solamente la differenza dei valori dei fattori di fase per i diversi cammini che determina il comportamento di un sistema.
Il particolare cammino per cui l'azione è un estremo - ![]() - o, come si dice più comunemente, il cammino di minima azione,
è l'unico cammino qcl(t) che una particella
segue in fisica classica. Nel caso quantistico, d'altra parte, tutte le
traiettorie contribuiscono all'integrale di cammino. Ciò che rende
qcl(t) particolare, è che esso è
il cammino per cui la fase è un estremo, quindi la differenza di
fase tra il cammino classico e quelli vicini cambia poco rapidamente.
- o, come si dice più comunemente, il cammino di minima azione,
è l'unico cammino qcl(t) che una particella
segue in fisica classica. Nel caso quantistico, d'altra parte, tutte le
traiettorie contribuiscono all'integrale di cammino. Ciò che rende
qcl(t) particolare, è che esso è
il cammino per cui la fase è un estremo, quindi la differenza di
fase tra il cammino classico e quelli vicini cambia poco rapidamente.
I cammini lontani da quello classico, non essendo in prossimità di un estremo per l'azione, hanno invece differenze di fase maggiori con quelli vicini. Perciò quando si sommano i contributi di tutti i cammini, solamente in vicinanza del cammino classico se ne trovano molti quasi in fase l'uno con l'altro, per cui si sommano costruttivamente, in modo coerente.
In situazioni per cui è ![]() ,
come nel caso classico di una particella macroscopica, le differenze di
fase sono più marcate, e questo fatto porta a selezionare la sola
traiettoria classica. Tuttavia, quando
,
come nel caso classico di una particella macroscopica, le differenze di
fase sono più marcate, e questo fatto porta a selezionare la sola
traiettoria classica. Tuttavia, quando ![]() ,
cioè nel caso quantistico, anche i cammini lontani da quello classico
possono essere ancora approssimativamente in fase, e contribuiscono tutti
alla somma. In questo caso il comportamento della particella non potrà
più essere adeguatamente descritto dalla fisica classica.
,
cioè nel caso quantistico, anche i cammini lontani da quello classico
possono essere ancora approssimativamente in fase, e contribuiscono tutti
alla somma. In questo caso il comportamento della particella non potrà
più essere adeguatamente descritto dalla fisica classica.
Il caso di un sistema con più gradi di libertà può essere trattato in modo analogo. Usando la notazione vettoriale:
| (2.31) |
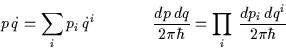 |
(2.32) |
si possono interpretare le formule precedenti anche per il caso multidimensionale.